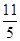题目内容
设 是椭圆
是椭圆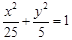 上一点,
上一点,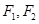 是椭圆的两个焦点,
是椭圆的两个焦点,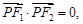
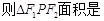 ( )
( )
A.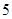 | B.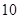 | C.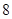 | D. |
A
解析试题分析:由椭圆方程可知 ,即
,即 ,
, 。因为
。因为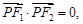 ,所以
,所以 ,所以
,所以 ,因为
,因为 ,解得
,解得 。因为
。因为 ,所以
,所以 。故A正确。
。故A正确。
考点:1椭圆的定义;2向量的数量积与向量垂直间的关系。

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
如图,菱形 的边长为
的边长为 ,
,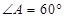 ,
, 为
为 的中点,若
的中点,若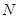 为菱形内任意一点(含边界),则
为菱形内任意一点(含边界),则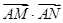 的最大值为( )
的最大值为( )
A. | B. | C. | D.9 |
平面向量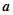 与
与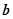 的夹角为60°,
的夹角为60°,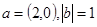 ,则
,则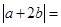 ( )
( )
A.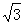 | B. | C.4 | D.12 |
 中,
中,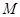 是线段
是线段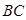 的中点且
的中点且 是线段
是线段 上一个动点,若
上一个动点,若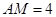 ,则
,则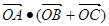 的最小值为( )
的最小值为( )
A.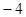 | B.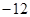 | C.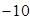 | D.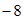 |
已知 、
、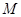 、
、 是单位圆上互不相同的三个点,且满足
是单位圆上互不相同的三个点,且满足 ,则
,则
的最小值是( )
A. | B. | C. | D. |
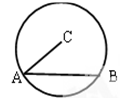
如图,半径为R的圆C中,已知弦AB的长为5,则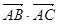 =( )
=( )
A.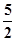 | B.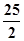 | C.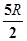 | D.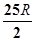 |
[2013·重庆诊测]若向量a=(1,λ,2),b=(2,-1,2),且a与b的夹角余弦值为 ,则λ等于( )
,则λ等于( )
| A.2 | B.-2 | C.-2或 | D.2或- |
 ,则
,则 的夹角为( )
的夹角为( )



 -t
-t )·
)·