Question

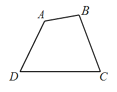
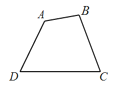
【题目】如图，在平面凸四边形中（凸四边形指没有角度数大于的四边形），.

（1）若，，求；

（2）已知，记四边形的面积为.

① 求的最大值；

② 若对于常数，不等式恒成立，求实数的取值范围.（直接写结果，不需要过程）

Answer 1

【答案】（1）3；（2）①；②.

【解析】

（1）在中，利用余弦定理求得；在中利用余弦定理构造关于的方程，解方程求得结果；（2）①在和中利用余弦定理构造等量关系可得，根据三角形面积公式可得，两式平方后作和可得，当时，可求得的最大值；②由可知，根据①可知，的范围由的范围决定，求解出且，且为钝角、为锐角；根据的单调性可求得最小值，从而求得得到结果.

（1）在中，，，

由余弦定理得：

在中，，，

由余弦定理得：

即：，解得：

（2）①在和中，由余弦定理得：

整理可得：

面积：，即：

即：

当时，即，时，

四边形面积的最大值为：

②

由①知：，则需研究的范围.

当增大时，增大，从而随之增大

所以，当趋于共线时，趋于，其中钝角满足

当减小时，减小，从而随之减小

所以，当趋于共线时，趋于，其中锐角满足

令，则在上递增，在上递减

并且，，

，即