题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,解不等式
,解不等式![]() ;
;
(Ⅱ)设![]() 是函数
是函数![]() 的四个不同的零点,问是否存在实数
的四个不同的零点,问是否存在实数![]() ,使得其中三个零点成等差数列?若存在,求出所有
,使得其中三个零点成等差数列?若存在,求出所有![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
(Ⅰ)先去绝对值,再解不等式;(Ⅱ)先求出两个已知零点,再讨论.
(Ⅰ)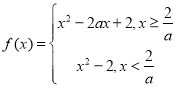
(1)当![]() 时,
时,![]() 即
即![]() 得
得![]()
若![]() 即
即![]() 时,不等式解集为
时,不等式解集为![]()
若![]() 即
即![]() 时,不等式解集为
时,不等式解集为![]()
(2)当![]() 时,
时,![]() 即
即![]()
若![]() 即
即![]() 时,
时,![]() 无解
无解
若![]() 即
即![]() 时
时
由![]() 得
得![]() ,
,
又![]() ,
, ![]()
![]() 不等式解集为
不等式解集为![]()
综上(1)(2)可知
当![]() 时,不等式的解集为
时,不等式的解集为![]()
当![]() 时,不等式的解集为
时,不等式的解集为![]()
(Ⅱ)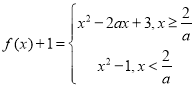 ,
,![]() 有4个不同零点
有4个不同零点
![]() ,
,![]()
不妨设![]() ,则
,则![]()
①若![]() 成等差数列,则
成等差数列,则![]() ,此时
,此时![]() ,不合题意
,不合题意
②若![]() 成等差数列,同①知不合题意
成等差数列,同①知不合题意
③若![]() 成等差数列,则
成等差数列,则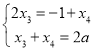 ,
,![]()
![]() ,
, ![]()
![]() 均舍去
均舍去
④若![]() 成等差数列,则
成等差数列,则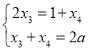
![]()
![]()
![]() ,
,![]() 或
或![]() (舍去)
(舍去)
综上可知:存在![]() 符合题意.
符合题意.

练习册系列答案
相关题目
【题目】已知圆![]() :
:![]() 与直线
与直线![]() :
:![]() ,动直线
,动直线![]() 过定点
过定点![]() .
.

(1)若直线![]() 与圆
与圆![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,点M是PQ的中点,直线
两点,点M是PQ的中点,直线![]() 与直线
与直线![]() 相交于点N.探索
相交于点N.探索![]() 是否为定值,若是,求出该定值;若不是,请说明理由.
是否为定值,若是,求出该定值;若不是,请说明理由.
【题目】已知某观光海域AB段的长度为3百公里,一超级快艇在AB段航行,经过多次试验得到其每小时航行费用Q(单位:万元)与速度v(单位:百公里/小时)(0≤v≤3)的以下数据:
| 0 | 1 | 2 | 3 |
| 0 | 0.7 | 1.6 | 3.3 |
为描述该超级快艇每小时航行费用Q与速度v的关系,现有以下三种函数模型供选择:Q=av3+bv2+cv,Q=0.5v+a,Q=klogav+b.
(1)试从中确定最符合实际的函数模型,并求出相应的函数解析式;
(2)该超级快艇应以多大速度航行才能使AB段的航行费用最少?并求出最少航行费用.