题目内容
两直线2x+y+2=0与ax+4y-2=0垂直，则其交点坐标为________．
（-1，0）
分析：根据两直线垂直，斜率之积等于-1，求出a=-2，把两直线的方程联立方程组求得交点的坐标．
解答：由题意可得-2×（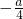
）=-1，∴a=-2．
两直线即2x+y+2=0与-8x+4y-2=0．
由
可得交点的坐标为（-1，0），
故答案为：（-1，0）．
点评：本题考查两直线垂直的性质，求两直线的交点坐标，属于基础题．
分析：根据两直线垂直，斜率之积等于-1，求出a=-2，把两直线的方程联立方程组求得交点的坐标．
解答：由题意可得-2×（
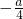）=-1，∴a=-2．两直线即2x+y+2=0与-8x+4y-2=0．
由
可得交点的坐标为（-1，0），故答案为：（-1，0）．
点评：本题考查两直线垂直的性质，求两直线的交点坐标，属于基础题．
练习册系列答案
相关题目