题目内容
考察下列三个命题，在“横线”处都缺少一个条件，补上这个条件使其构成真命题（其中l?m为直线，α?β为平面），则此条件为 ．
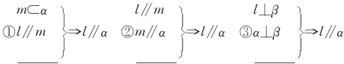
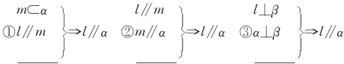
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：根据线面平行的判定定理，我们知道要判断线面平行需要三个条件：面内一线，面外一线，线线平行，分析已知中的三个命题，即可得到答案．
解答：
解：①体现的是线面平行的判定定理，
缺的条件是“l为平面α外的直线”，
即“l?α”．
它同样适合②③，
故填l?α．
故答案为：l?α．
缺的条件是“l为平面α外的直线”，
即“l?α”．
它同样适合②③，
故填l?α．
故答案为：l?α．
点评：本题考查的知识点是直线与平面平行的判定，熟练掌握直线与平面平行判断的方法及必要的条件是解答本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，线段AB夹在一个直二面角的两个半平面内，它与两个半平面所成角都是30°，则AB与这个二面角的棱l所成角为（ ）| A、30° | B、45° |
| C、60° | D、90° |
已知不等式|x-m|＜1成立的一个充分非必要条件是
＜x＜
，则实数m的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、(-∞，-
| ||||
D、[
|
如图，在△ABC中，DE∥BC，BE∥DF，若BC=4．DE=3，EF=1，则EC的长为平面内△ABC及一点O满足
•
=
•
，
•
=
•
，则点O是△ABC的（ ）
| AO |
| AB |
| BO |
| BA |
| BO |
| BC |
| CO |
| CB |
| A、重心 | B、垂心 | C、内心 | D、外心 |