Question

【题目】已知函数，．

(1)若函数是奇函数，求实数的值；

(2)在(1)的条件下，判断函数与函数的图象公共点个数，并说明理由；

(3)当时，函数的图象始终在函数的图象上方，求实数的取值范围．

Answer 1

【答案】(1) .

(2) 函数与函数的图象有2个公共点；说明见解析.

(3).

【解析】分析：（1）由题意可得，解出；

（2）要求方程解的个数，即求方程在定义域上的解的个数，令，利用零点存在定理判断即可；

（3）要使时，函数的图象始终在函数的图象的上方，

必须使在上恒成立，令，则，上式整理得在恒成立，分类讨论即可.

详解：（1）因为为奇函数，所以对于定义域内任意，都有，

即，

，

显然，由于奇函数定义域关于原点对称，所以必有.

上面等式左右两边同时乘以得

，化简得

，.

上式对定义域内任意恒成立，所以必有，

解得.

（2）由（1）知，所以，即，

由得或，

所以函数定义域.

由题意，要求方程解的个数，即求方程

在定义域上的解的个数.

令，显然在区间和均单调递增，

又，

且，.

所以函数在区间和上各有一个零点，

即方程在定义域上有2个解，

所以函数与函数的图象有2个公共点.

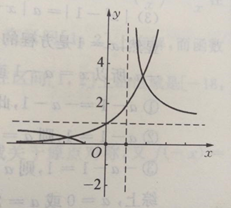
（附注：函数与在定义域上的大致图象如图所示）

（3）要使时，函数的图象始终在函数的图象的上方，

必须使在上恒成立，

令，则，上式整理得在恒成立.

方法一：令，.

① 当，即时，在上单调递增，

所以，恒成立；

② 当，即时，在上单调递减，

只需，解得与矛盾.

③ 当，即时，

在上单调递减，在上单调递增，

所以由，解得，

又，所以

综合①②③得的取值范围是.

方法二：因为在恒成立. 即，

又，所以得在恒成立

令，则，且，

所以，

由基本不等式可知（当且仅当时，等号成立.）

即，

所以,

所以的取值范围是.