题目内容
【题目】如图,在![]() 中,点
中,点![]() 在
在![]() 边上,
边上,![]() ,
,![]() ,
,![]() ,
,![]() .
.
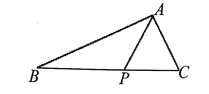
(1)求![]() 的值;
的值;
(2)若![]() 的面积是
的面积是![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)在![]() 中,由余弦定理得
中,由余弦定理得![]() ,解得
,解得![]() ,再由正弦定理即可得出答案;
,再由正弦定理即可得出答案;
(2)利用三角形面积公式可求![]() ,进而利用余弦定理可求AB.
,进而利用余弦定理可求AB.
详解:(1)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,
![]()
整理得![]() ,解得
,解得![]() 或
或![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
由正弦定理![]() 得
得 ![]() ,
,
解得![]() .
.
(2)因为![]() ,由(1)知
,由(1)知![]() ,
,![]() .
.
所以![]() 的面积
的面积![]() ,
,
又![]() 的面积是
的面积是![]() ,
,
所以![]() 的面积
的面积![]()
由(1)知![]() ,
,
![]() ,
,
解得![]() ,
,
又因为![]() ,所以
,所以![]() 必为锐角,
必为锐角,
![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,![]()
![]()
![]()
(1)解法2:设![]() ,在
,在![]() 中,由正弦定理得
中,由正弦定理得![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]()
(2)解法2:由(1)知![]() ,在
,在![]() 中,由正弦定理得
中,由正弦定理得![]()
解得![]() ,
,![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得![]() ,
,
![]() ,
,
![]()
又![]() 的面积是
的面积是![]() ,
,
![]() ,
,
解得![]() ,
,
在![]() 中,由余弦定理得,
中,由余弦定理得,
![]() ,
,
![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目