题目内容
已知函数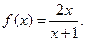
(1)当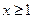 时, 证明: 不等式
时, 证明: 不等式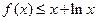 恒成立;
恒成立;
(2)若数列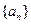 满足
满足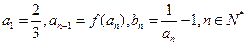 ,证明数列
,证明数列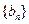 是等比数列,并求出数列
是等比数列,并求出数列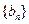 、
、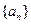 的通项公式;
的通项公式;
(3)在(2)的条件下,若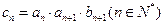 ,证明:
,证明: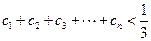 .
.
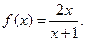
(1)当
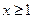 时, 证明: 不等式
时, 证明: 不等式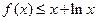 恒成立;
恒成立; (2)若数列
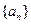 满足
满足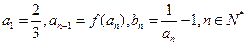 ,证明数列
,证明数列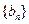 是等比数列,并求出数列
是等比数列,并求出数列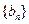 、
、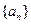 的通项公式;
的通项公式; (3)在(2)的条件下,若
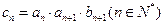 ,证明:
,证明: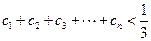 .
.(1)证明略
(2) ,
,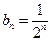 ,
,
(3)证明略
(2)
 ,
,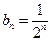 ,
,(3)证明略
(1)方法一:∵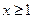 ,
,
∴
而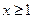 时,
时,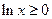 ,∴
,∴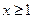 时,
时,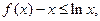
∴当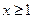 时,
时,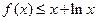 恒成立.
恒成立.
方法二:令 ,
,
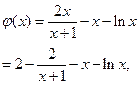

故 是定义域
是定义域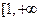 )上的减函数,
)上的减函数,
∴当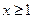 时,
时, 恒成立.
恒成立.
即当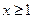 时,
时,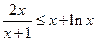 恒成立.
恒成立.
∴当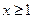 时,
时,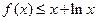 恒成立. ……4分
恒成立. ……4分
(2)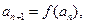 ∴
∴
∵ ∴
∴
 ,
,
又
∴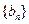 是首项为
是首项为 ,公比为
,公比为 的等比数列,其通项公式为
的等比数列,其通项公式为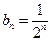 .
.
又
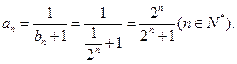 ……10分
……10分
(3)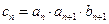
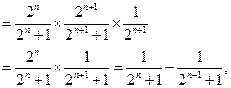 W$
W$
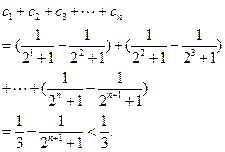
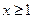 ,
,∴

而
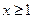 时,
时,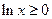 ,∴
,∴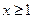 时,
时,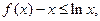
∴当
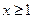 时,
时,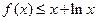 恒成立.
恒成立.方法二:令
 ,
,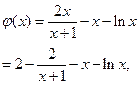

故
 是定义域
是定义域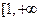 )上的减函数,
)上的减函数,∴当
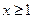 时,
时, 恒成立.
恒成立.即当
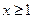 时,
时,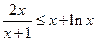 恒成立.
恒成立.∴当
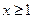 时,
时,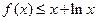 恒成立. ……4分
恒成立. ……4分(2)
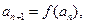 ∴
∴
∵
 ∴
∴
 ,
,又

∴
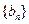 是首项为
是首项为 ,公比为
,公比为 的等比数列,其通项公式为
的等比数列,其通项公式为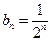 .
.又

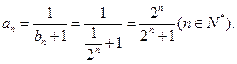 ……10分
……10分(3)
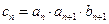
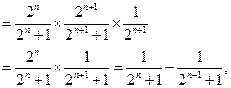 W$
W$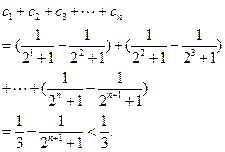

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
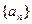 }满足:
}满足: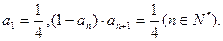
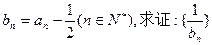 为等差数列;
为等差数列;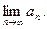
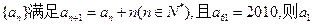 =" " ( )
=" " ( )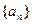 的前m项和为30,前2m项和为100,则它的前3m项的和为 ( )
的前m项和为30,前2m项和为100,则它的前3m项的和为 ( )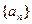 的前n项和为
的前n项和为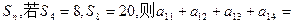 ( )
( )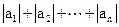 ,求Sn
,求Sn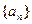 中,首项
中,首项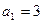 ,前三项和为
,前三项和为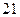 ,则
,则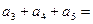
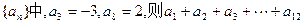 =" " ( )
=" " ( )