题目内容
设log3a=log2b=( )c=(
)c=( )d<
)d< ,则a、b、c、d大小关系为
,则a、b、c、d大小关系为
- A.a>b>c>d
- B.a>b>d>c
- C.c>d>a>b
- D.d>c>a>b
D
分析:令log3a=log2b=( )c=(
)c=( )d=k,利用幂函数的单调性判断a,b的大小,根据指数函数的单调性判断a与3的大小,根据指数函数的单调性判断c,d与3的大小,进而得到答案.
)d=k,利用幂函数的单调性判断a,b的大小,根据指数函数的单调性判断a与3的大小,根据指数函数的单调性判断c,d与3的大小,进而得到答案.
解答:令log3a=log2b=( )c=(
)c=( )d=k
)d=k
则0<k< ,
,
则y=xk为增函数
则a=3k,b=2k,
即a>b
又由y=3x为增函数
a=3k<31
故a<3
即3>a>b
而C=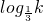 =
=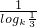 ,d=
,d=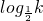 =
=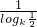
由y=logkx为减函数
故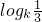 >
>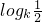
故d>c
又∵0<k<
∴c=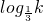 >
>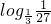 =3
=3
故d>c>3
故d>c>a>b
故选D
点评:本题考查的知识点是对数函数的单调性,指数函数的单调性,不等式比较大小,其中熟练掌握指数函数,对数函数,幂函数的单调性是解答本题的关键.
分析:令log3a=log2b=(
 )c=(
)c=( )d=k,利用幂函数的单调性判断a,b的大小,根据指数函数的单调性判断a与3的大小,根据指数函数的单调性判断c,d与3的大小,进而得到答案.
)d=k,利用幂函数的单调性判断a,b的大小,根据指数函数的单调性判断a与3的大小,根据指数函数的单调性判断c,d与3的大小,进而得到答案.解答:令log3a=log2b=(
 )c=(
)c=( )d=k
)d=k则0<k<
 ,
,则y=xk为增函数
则a=3k,b=2k,
即a>b
又由y=3x为增函数
a=3k<31
故a<3
即3>a>b
而C=
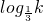 =
=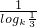 ,d=
,d=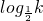 =
=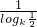
由y=logkx为减函数
故
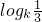 >
>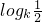
故d>c
又∵0<k<

∴c=
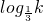 >
>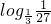 =3
=3故d>c>3
故d>c>a>b
故选D
点评:本题考查的知识点是对数函数的单调性,指数函数的单调性,不等式比较大小,其中熟练掌握指数函数,对数函数,幂函数的单调性是解答本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 )c=(
)c=( )d<
)d<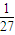 ,则a、b、c、d大小关系为( )
,则a、b、c、d大小关系为( )