Question

下列函数中是奇函数的为（ ）
A．y=x²+cosx，x∈R
B．y=|2sinx|，x∈R
C．y=tanx²，x≠±
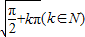
D．y=x²sinx，x∈R

Answer 1

【答案】分析：利用函数奇偶性的定义分别判断即可，主要函数的定义域是否关于原点对称．
解答：解；A．因为f（-x）=（-x）²+cos（-x）=x²+cosx=f（x），所以A为偶函数．
B．因为f（-x）=|2sin（-x）|=|2sinx|=f（x），所以B为偶函数．
C．因为f（-x）=tan（-x）²=tanx²=f（x），所以C为偶函数．
D．因为f（-x）=（-x）²sin（-x）=-x²sinx=-f（x），所以D为奇函数．
故选D．
点评：本题主要考查函数奇偶性的判断，要求熟练掌握常见基本函数的奇偶性．