题目内容
已知圆C：
，直线l：
．
（1）证明：不论m取什么实数时，直线l与圆恒交于两点；
（2）求直线l被圆C截得的线段的最短长度以及此时直线l的方程．
（1）证明见解析。
（2）线段的最短长度
，
解析:
(1) 由
知直线l恒过定点
又
∴ 直线l恒过定点A（3，1），
且
A（3，1）必在圆内，故直线l与圆恒有两交点．
(2) ∵ 圆心为C（1，2），定点为A（3，1） ∴ 
由平面几何知识知，当直线l与AC垂直时所截线段最短，此时
∴ l方程为：，此时
∴ 最短弦长
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
相关题目
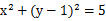，直线l：
（m∈R）． （Ⅰ）证明：不论m取什么实数，直线l与圆恒交于两点．
，直线L：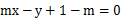
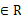，直线L与圆C总有两个交点；
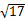，求直线L的倾斜角；
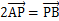,求此时直线L的方程.
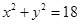，直线l：
则圆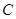
上任一点到直线
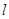的距离小于2的概率为
.
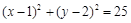，直线l：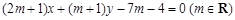
．