题目内容
已知圆C：
，直线l：
（m∈R）． （Ⅰ）证明：不论m取什么实数，直线l与圆恒交于两点．
（Ⅱ）求直线被圆C截得的弦长最小时l的方程．
（2）2x－y－５＝0
解析:
（Ⅰ）证明：直线l：
可化为
由于m∈R，则
，解得
，
∴直线l经过定点A（3，1）.
又∵ 圆C的圆心坐标为（1，2），且│AC│＝
＜５（半径），
∴ 点A在圆C内，
从而不论m为何值，直线l恒与圆C相交于两点．
（Ⅱ）解：要使弦长最小时，必须l⊥AC，
??由kBC＝－
，知k1＝2，m＝－
．
??所以直线l的方程为2x－y－５＝0．
练习册系列答案
考前必练系列答案
相关题目
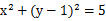，直线l：
．
，直线L：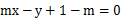
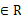，直线L与圆C总有两个交点；
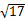，求直线L的倾斜角；
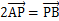,求此时直线L的方程.
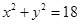，直线l：
则圆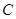
上任一点到直线
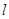的距离小于2的概率为
.
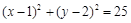，直线l：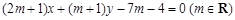
．