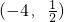题目内容
已右集合M={x|x2+3x-4<4},N={x|22x-1>1}则M∩N=( )A.(-4,1)
B.

C.

D.(1,+∞)
【答案】分析:先利用一元二次不等式的解法化简集合A,再利用指数函数的单调性化简集合B,最后求出它们的交集即可.
解答:解:∵M={x|x2+7x-4<4}
={x|-8<x<1},
又∵N={x|22x-1>1}={x|x> }
}
∴M∩N= .
.
故选C.
点评:本题主要考查了一元二次不等式的解法、指数函数的单调性、交集及其运算,是一道基础题.
解答:解:∵M={x|x2+7x-4<4}
={x|-8<x<1},
又∵N={x|22x-1>1}={x|x>
 }
}∴M∩N=
 .
.故选C.
点评:本题主要考查了一元二次不等式的解法、指数函数的单调性、交集及其运算,是一道基础题.

练习册系列答案
相关题目
已右集合M={x|x2+7x-4<4},N={x|22x-1>1}则M∩N=( )
| A、(-4,1) | ||
B、(-4,
| ||
C、(
| ||
| D、(1,+∞) |