题目内容
已知O是坐标原点,点A(2,0),△AOC的顶点C在曲线y2=4(x-1)上,那么△AOC的重心G的轨迹方程是( )
| A.3y2=4(x-1) | B.3y2=4(x-1)(y≠0) | ||||
C.
| D.
|
设G(x,y),C(m,n),
则
(y≠0),
∴m=3x-2,n=3y,
∵△AOC的顶点C在曲线y2=4(x-1)上,
∴(3y)2=4(
-1),
即3y2=4(x-1)(y≠0),
∴△AOC的重心G的轨迹方程是3y2=4(x-1)(y≠0).
故选B.
则
|
∴m=3x-2,n=3y,
∵△AOC的顶点C在曲线y2=4(x-1)上,
∴(3y)2=4(
| 2+m |
| 3 |
即3y2=4(x-1)(y≠0),
∴△AOC的重心G的轨迹方程是3y2=4(x-1)(y≠0).
故选B.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 中,设椭圆
中,设椭圆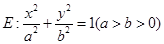 ,其中
,其中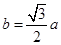 ,过椭圆
,过椭圆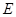 内一点
内一点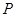
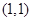 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点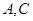 和
和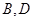 ,且满足
,且满足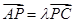 ,
,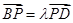 ,其中
,其中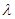 为正常数. 当点
为正常数. 当点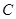 恰为椭圆的右顶点时,对应的
恰为椭圆的右顶点时,对应的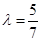 .
.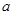 与
与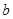 的值;
的值;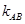 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.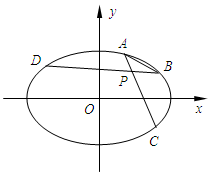
 =2
=2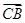 ,则点C的轨迹是( )
,则点C的轨迹是( )