题目内容
4.一同学在电脑中打出如图若干个圆(○表示空心圆,●表示实心圆)○●○○●○○○●○○○○●○○○○○●○…到1000个圆中有43个实心圆.
分析 根据题意,把圆分组,利用等差数列的定义与前n项和公式,通过归纳推理,即可求出结论.
解答 解:根据题意,把圆分组如下;
第一组,○●,2个;
第二组,○○●,3个;
第三组,○○○●,4个;
第四组,○○○○●,5个;
第五组,○○○○○●,6个;…,
第n组,n+1个;
每组的最后一个为实心圆,且每组的总个数组成等差数列,
其前n项和为Sn=2+3+4+5+…+(n+1)=$\frac{n(n+3)}{2}$;
又$\frac{43×46}{2}$=989<1000,$\frac{44×47}{2}$=1034>1000,
所以在前1000个圆圈中包含43个整组,第44组的一部分;
所以有43个实心圆.
故答案为:43.
点评 本题考查了归纳推理能力的应用问题,也考查了等差数列前n项和的应用问题,是基础题目.

练习册系列答案
相关题目
15.设函数f(x)=cos2x-2sinxcosx-sin2x,g(x)=2cos2x+2sinxcosx-1,把f(x)的图象向右平移m个单位后,图象恰好为函数g(x)的图象,则m的值可以是( )
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
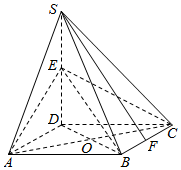 如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.
如图,四棱锥S-ABCD底面是正方形,SD⊥平面ABCD,SD=AD=2,点E是SD的中点,F是BC线段上的点,O是AC与BD的交点.