��Ŀ����
10����֪����{an}�ĸ���Ϊ��������ǰn���ΪSn����${S_n}={��\frac{{{a_n}+1}}{2}��^2}$����bn=10-an��n��N������1����֤������{an}�ǵȲ����У�����{an}��ͨ�ʽ��
��2��������{bn}��ǰn���ΪTn����Tn�����ֵ��
��3��������{bn}��ͨ�ʽΪ${b_n}=\frac{a_n}{{{a_n}+t}}$���ʣ��Ƿ����������t��ʹ��b1��b2��bm��m��3��m��N���ɵȲ����У������ڣ����t��m��ֵ���������ڣ���˵�����ɣ�
���� ��1����n=1ʱ��${a_1}={S_1}={��\frac{{{a_1}+1}}{2}��^2}$�����a1=1����n��2ʱ��an=Sn-Sn-1����Ϊ��an+an-1����an-an-1-2��=0������֪�ɵã�an-an-1-2=0�����õȲ����е�ͨ�ʽ���ɵó���
��2��bn=10-an=-2n+11���ɵ�{bn}�ǵȲ����У��������ʽ�����κ����ĵ����Լ��ɵó���
��3���ɣ�1��֪${b_n}=\frac{2n-1}{2n-1+t}$��Ҫʹb1��b2��bm�ɵȲ����У��ɵ�2b2=b1+bm�����뻯�ɵó���
��� �⣺��1����n=1ʱ��${a_1}={S_1}={��\frac{{{a_1}+1}}{2}��^2}$����a1=1����2�֣�
��n��2ʱ��an=Sn-Sn-1=$��\frac{{a}_{n}+1}{2}��^{2}$-$��\frac{{a}_{n-1}+1}{2}��^{2}$������an+an-1����an-an-1-2��=0��
������{an}�ĸ���Ϊ��������an+an-1��0��an-an-1-2=0��
����{an}�ǵȲ����У�����Ϊ2��
��an=1+2��n-1��=2n-1��
��2��bn=10-an=-2n+11��b1=9��
��bn-bn-1=-2����{bn}�ǵȲ����С���7�֣�
��${T_n}=\frac{{n��{b_1}+{b_n}��}}{2}=-{n^2}+10n$����n=5ʱ��${T_{nmax}}=-{5^2}+10��5=25$����10�֣�
��3���ɣ�1��֪${b_n}=\frac{2n-1}{2n-1+t}$��Ҫʹb1��b2��bm�ɵȲ����У�
��2b2=b1+bm����$2��\frac{3}{3+t}=\frac{1}{1+t}+\frac{2m-1}{2m-1+t}$������������$m=3+\frac{4}{t-1}$����1��2�֣�
��Ϊm��tΪ������������tֻ��ȡ2��3��5��
��t=2ʱ��m=7����t=3ʱ��m=5����t=5ʱ��m=4��
�ʴ���������t��ʹ��b1��b2��bm�ɵȲ����У�����16�֣�
���� ���⿼�������е��ƹ�ϵ���Ȳ����е�ͨ�ʽ�����ʽ�����κ����ĵ����ԣ����̵Ľⷨ��������������������������������е��⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�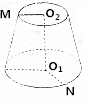 ��ͼ��Բ̨�ĸ�Ϊ4���ϡ��µ���뾶�ֱ�Ϊ3��5��M��N�ֱ����ϡ��µ���Բ���ϣ��ң�$\overrightarrow{{O}_{2}M}$��$\overrightarrow{{O}_{1}N}$��=120�㣬��|$\overrightarrow{MN}$|���ڣ�������
��ͼ��Բ̨�ĸ�Ϊ4���ϡ��µ���뾶�ֱ�Ϊ3��5��M��N�ֱ����ϡ��µ���Բ���ϣ��ң�$\overrightarrow{{O}_{2}M}$��$\overrightarrow{{O}_{1}N}$��=120�㣬��|$\overrightarrow{MN}$|���ڣ�������| A�� | $\sqrt{65}$ | B�� | 5$\sqrt{2}$ | C�� | $\sqrt{35}$ | D�� | 5 |
 ��֪����S-ABCD�ĵ���Ϊƽ���ı��Σ���SD��ƽ��ABCD��AB=2AD=2SD����DCB=60�㣬M��N�ֱ�ΪSB��SC���е㣬��MN��ƽ��MNPQ�ֱ����߶�CD��AB�ཻ�ڵ�P��Q����$\overrightarrow{AQ}=��\overrightarrow{AB}$��
��֪����S-ABCD�ĵ���Ϊƽ���ı��Σ���SD��ƽ��ABCD��AB=2AD=2SD����DCB=60�㣬M��N�ֱ�ΪSB��SC���е㣬��MN��ƽ��MNPQ�ֱ����߶�CD��AB�ཻ�ڵ�P��Q����$\overrightarrow{AQ}=��\overrightarrow{AB}$��