题目内容
设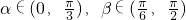 ,且α,β满足
,且α,β满足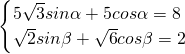
(1)求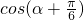 的值.
的值.
(2)求cos(α+β)的值.
解:(1)∵5 sinα+5cosα=8,
sinα+5cosα=8,
∴10( sinα+
sinα+ cosα)=8,即sin(α+
cosα)=8,即sin(α+ )=
)= ,(3分)
,(3分)
∵α∈(0, ),∴α+
),∴α+ ∈(
∈( ,
, ),
),
∴cos(α+ )=
)=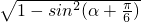 =
= ;(4分)
;(4分)
(2)又∵ sinβ+
sinβ+ cosβ=2,
cosβ=2,
∴2 (
( sinβ+
sinβ+ cosβ)=2,即sin(β+
cosβ)=2,即sin(β+ )=
)= ,(6分)
,(6分)
∵β∈( ,
, ),∴β+
),∴β+ ∈(
∈( ,
, ),
),
∴cos(β+ )=-
)=- ,(7分)
,(7分)
∴cos(α+β)=sin[ +(α+β)]=sin[(α+
+(α+β)]=sin[(α+ )+(β+
)+(β+ )]
)]
=sin(α+ )cos(β+
)cos(β+ )+cos(α+
)+cos(α+ )sin(β+
)sin(β+ )
)
= ×(-
×(- )+
)+ ×
× =-
=- .(12分)
.(12分)
分析:(1)将等式5 sinα+5cosα=8左边提取10,利用两角和与差的正弦函数公式及特殊角的三角函数值求出sin(α+
sinα+5cosα=8左边提取10,利用两角和与差的正弦函数公式及特殊角的三角函数值求出sin(α+ )的值,由α的范围求出α+
)的值,由α的范围求出α+ 的范围,利用同角三角函数间的基本关系化简即可求出cos(α+
的范围,利用同角三角函数间的基本关系化简即可求出cos(α+ )的值;
)的值;
(2)等式 sinβ+
sinβ+ cosβ=2左边提取2
cosβ=2左边提取2 ,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,求出sin(β+
,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,求出sin(β+ )的值,由β的范围求出β+
)的值,由β的范围求出β+ 的范围,利用同角三角函数间的基本关系求出cos(β+
的范围,利用同角三角函数间的基本关系求出cos(β+ )的值,将所求式子利用诱导公式sin(
)的值,将所求式子利用诱导公式sin( +θ)=cosθ变形,其中的角
+θ)=cosθ变形,其中的角 +α+β变形为(α+
+α+β变形为(α+ )+(β+
)+(β+ ),利用两角和与差的正弦函数公式化简后,将各自的值代入即可求出值.
),利用两角和与差的正弦函数公式化简后,将各自的值代入即可求出值.
点评:此题考查了两角和与差的正弦函数公式,诱导公式,同角三角函数间的基本关系,熟练掌握公式,灵活变换角度是解本题的关键,同时注意角度的范围.本题中灵活运用角的变换的技巧达到了用已知表示未知,在求值题中,这是一个重要的经验!
 sinα+5cosα=8,
sinα+5cosα=8,∴10(
 sinα+
sinα+ cosα)=8,即sin(α+
cosα)=8,即sin(α+ )=
)= ,(3分)
,(3分)∵α∈(0,
 ),∴α+
),∴α+ ∈(
∈( ,
, ),
),∴cos(α+
 )=
)=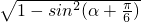 =
= ;(4分)
;(4分)(2)又∵
 sinβ+
sinβ+ cosβ=2,
cosβ=2,∴2
 (
( sinβ+
sinβ+ cosβ)=2,即sin(β+
cosβ)=2,即sin(β+ )=
)= ,(6分)
,(6分)∵β∈(
 ,
, ),∴β+
),∴β+ ∈(
∈( ,
, ),
),∴cos(β+
 )=-
)=- ,(7分)
,(7分)∴cos(α+β)=sin[
 +(α+β)]=sin[(α+
+(α+β)]=sin[(α+ )+(β+
)+(β+ )]
)]=sin(α+
 )cos(β+
)cos(β+ )+cos(α+
)+cos(α+ )sin(β+
)sin(β+ )
)=
 ×(-
×(- )+
)+ ×
× =-
=- .(12分)
.(12分)分析:(1)将等式5
 sinα+5cosα=8左边提取10,利用两角和与差的正弦函数公式及特殊角的三角函数值求出sin(α+
sinα+5cosα=8左边提取10,利用两角和与差的正弦函数公式及特殊角的三角函数值求出sin(α+ )的值,由α的范围求出α+
)的值,由α的范围求出α+ 的范围,利用同角三角函数间的基本关系化简即可求出cos(α+
的范围,利用同角三角函数间的基本关系化简即可求出cos(α+ )的值;
)的值;(2)等式
 sinβ+
sinβ+ cosβ=2左边提取2
cosβ=2左边提取2 ,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,求出sin(β+
,利用两角和与差的正弦函数公式及特殊角的三角函数值化简,求出sin(β+ )的值,由β的范围求出β+
)的值,由β的范围求出β+ 的范围,利用同角三角函数间的基本关系求出cos(β+
的范围,利用同角三角函数间的基本关系求出cos(β+ )的值,将所求式子利用诱导公式sin(
)的值,将所求式子利用诱导公式sin( +θ)=cosθ变形,其中的角
+θ)=cosθ变形,其中的角 +α+β变形为(α+
+α+β变形为(α+ )+(β+
)+(β+ ),利用两角和与差的正弦函数公式化简后,将各自的值代入即可求出值.
),利用两角和与差的正弦函数公式化简后,将各自的值代入即可求出值.点评:此题考查了两角和与差的正弦函数公式,诱导公式,同角三角函数间的基本关系,熟练掌握公式,灵活变换角度是解本题的关键,同时注意角度的范围.本题中灵活运用角的变换的技巧达到了用已知表示未知,在求值题中,这是一个重要的经验!

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目