题目内容

已知抛物线y2=4ax(0＜a＜1)的焦点为F，以A(a+4,0)为圆心，｜AF｜为半径在x轴上方作半圆交抛物线于不同的两点M和N，设P为线段MN的中点，

(Ⅰ)求｜MF｜+｜NF｜的值；

(Ⅱ)是否存在这样的a值，使｜MF｜、｜PF｜、｜NF｜成等差数列?如存在，求出a的值，

(1) 8    (2)不存在


解析:

(1)由已知得F(a,0),半圆为［x-(a+4)］2+y2=16(y≥0)，设M(x1,y1),N(x2,y2)，则｜MF｜+｜NF｜=x1+x2+2a=2(4-a)+2a=8

(2)若｜MF｜、｜PF｜、｜NF｜成等成数列，则有2｜PF｜=｜MF｜+｜NF｜,另一方面，设M、P、N在抛物线的准线上的射影为M′、P′、N′，则在直角梯形M′MNN′中，P′P是中位线，又有2｜P′P｜=｜M′M｜+｜N′N｜=｜MF｜+｜FN｜,因而｜PF｜=｜P′P｜,∴P点应在抛物线上，但P点是线段MN的中点，即P并不在抛物线上，故不存在使｜MF｜、｜PF｜、｜NF｜成等差数列的a值.

练习册系列答案
相关题目
已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．
（2003•东城区二模）已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（Ⅰ）求点P和Q的坐标；
（Ⅱ）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程；
（Ⅲ）设点A（t，0）（常数t＞4），当a在闭区间〔1，2〕内变化时，求△APQ面积的最大值，并求相应a的值．
已知抛物线y2=4a（x+a）（a＞0），过原点O作一直线交抛物线于A、B两点，如图所示，试求|OA|·|OB|的最小值。
已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为
2
，过抛物线C1的焦点F作倾斜角为
π
4
的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．
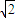已知抛物线C1：y2=4ax（a＞0），椭圆C以原点为中心，以抛物线C1的焦点为右焦点，且长轴与短轴之比为，过抛物线C1的焦点F作倾斜角为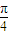的直线l，交椭圆C于一点P（点P在x轴上方），交抛物线C1于一点Q（点Q在x轴下方）．
（1）求点P和Q的坐标；
（2）将点Q沿直线l向上移动到点Q′，使|QQ′|=4a，求过P和Q′且中心在原点，对称轴是坐标轴的双曲线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网