题目内容
已知抛物线C1:y2=4ax(a>0),椭圆C以原点为中心,以抛物线C1的焦点为右焦点,且长轴与短轴之比为| 2 |
| π |
| 4 |
(1)求点P和Q的坐标;
(2)将点Q沿直线l向上移动到点Q′,使|QQ′|=4a,求过P和Q′且中心在原点,对称轴是坐标轴的双曲线的方程.
分析:(1)设椭圆方程,进而根据题意求得a和m,a和n的关系,进而根据椭圆方程与直线l联立求得交点坐标.
(2)将Q点沿直线l向上移动到Q′点,使|QQ′|=4a,则可求出Q′点的坐标,设双曲线方程,把P,Q′代入双曲线方程,求得s和r,进而双曲线方程可得.
(2)将Q点沿直线l向上移动到Q′点,使|QQ′|=4a,则可求出Q′点的坐标,设双曲线方程,把P,Q′代入双曲线方程,求得s和r,进而双曲线方程可得.
解答:解:(1)由题意可知F(a,0),设椭圆方程为
+
=1(m>n>0).
由
=
,m2-n2=a2,
解得m2=2a2,n2=a2,
∴椭圆方程为
+
=1,直线l:y=x-a.
可求出P(
a,
a).
y=x-a,
可求出Q((3-2
)a,(2-2
)a.
(2)将Q点沿直线l向上移动到Q′点,
使|QQ′|=4a,则可求出Q′点的坐标为(3a,2a).
设双曲线方程为
-
=1(s•r>0).
由于P、Q′在双曲线上,则有
-
=1,
-
=1.
解得
=
,
=
.
∴双曲线方程为
x2-
y2=1.
| x2 |
| m2 |
| y2 |
| n2 |
由
| m |
| n |
| 2 |
解得m2=2a2,n2=a2,
∴椭圆方程为
| x2 |
| 2a2 |
| y2 |
| a2 |
可求出P(
| 4 |
| 3 |
| 1 |
| 3 |
y=x-a,
可求出Q((3-2
| 2 |
| 2 |
(2)将Q点沿直线l向上移动到Q′点,
使|QQ′|=4a,则可求出Q′点的坐标为(3a,2a).
设双曲线方程为
| x2 |
| s |
| y2 |
| r |
由于P、Q′在双曲线上,则有
| (3a)2 |
| s |
| (2a)2 |
| r |
(
| ||
| s |
(
| ||
| r |
解得
| 1 |
| s |
| 7 |
| 11a2 |
| 1 |
| r |
| 13 |
| 11a2 |
∴双曲线方程为
| 7 |
| 11a2 |
| 13 |
| 11a2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生对圆锥曲线基本知识的综合掌握.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 (2012•河北模拟)已知抛物线C1:y2=2px和圆
(2012•河北模拟)已知抛物线C1:y2=2px和圆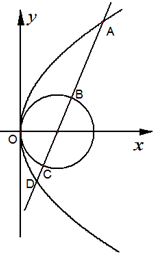 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).