题目内容
设函数f(x)=sinxcosx+cos2x.
(1)求f(x)的最小正周期;
(2)当x∈[0,
]时,求函数f(x)的最大值和最小值.
(1)求f(x)的最小正周期;
(2)当x∈[0,
| π | 2 |
分析:(1)先利用二倍角公式和两角和的正弦公式将函数f(x)化为y=Asin(ωx+φ)的形式,再利用周期计算公式求其最小正周期即可
(2)先求内层函数2x+
的值域,在将其看做整体,利用正弦函数的图象和性质求函数的最值即可
(2)先求内层函数2x+
| π |
| 4 |
解答:解:f(x)=sinxcosx+cos2x=
sin2x+
(1+cos2x)=
sin(2x+
)+
.
(1)∴f(x)的最小正周期T=
=π
(2)∵x∈[0,
],∴2x+
∈[
,
]
∴sin(2x+
)∈[-
,1]
∴f(x)=
sin(2x+
)+
∈[0,
]
∴函数f(x)的最大值为
,最小值为0
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
(1)∴f(x)的最小正周期T=
| 2π |
| 2 |
(2)∵x∈[0,
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴sin(2x+
| π |
| 4 |
| ||
| 2 |
∴f(x)=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
∴函数f(x)的最大值为
| ||
| 2 |
点评:本题主要考查了y=Asin(ωx+φ)型函数的图象和性质,三角变换公式在解决三角化简和求值问题中的作用,复合函数最值的求法,整体代入的思想方法

练习册系列答案
相关题目
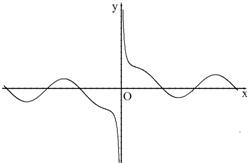 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=| 1 |
| x |
A、
| ||
| B、f(x)g(x) | ||
| C、f(x)-g(x) | ||
| D、f(x)+g(x) |
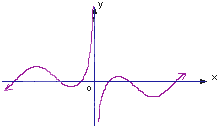 设函数f(x)=sinx,g(x)=
设函数f(x)=sinx,g(x)=