题目内容
已知函数f(x)满足f(x3-1)=
思路分析一:欲求f′(x),需先求f(x),用换元法求解.
解法一:令t=x3-1,则x=![]() .
.
∴f(x)=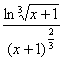 .∴f′(x)=
.∴f′(x)=![]() .
.
思路分析二:依据复合函数的求导法则进行求解.
解法二:y=f(x3-1)可看成是由y=f(t),t=x3-1复合而成的.对原式两边求导,
得f′(t)·(x3-1)′=![]() .
.
∴f′(t)=![]() .把x=
.把x=![]() 代入该表达式,可得f′(t)=
代入该表达式,可得f′(t)=![]() ,
,
即f′(x)=![]() .
.

练习册系列答案
相关题目
题目内容
已知函数f(x)满足f(x3-1)=
思路分析一:欲求f′(x),需先求f(x),用换元法求解.
解法一:令t=x3-1,则x=![]() .
.
∴f(x)=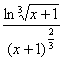 .∴f′(x)=
.∴f′(x)=![]() .
.
思路分析二:依据复合函数的求导法则进行求解.
解法二:y=f(x3-1)可看成是由y=f(t),t=x3-1复合而成的.对原式两边求导,
得f′(t)·(x3-1)′=![]() .
.
∴f′(t)=![]() .把x=
.把x=![]() 代入该表达式,可得f′(t)=
代入该表达式,可得f′(t)=![]() ,
,
即f′(x)=![]() .
.
