题目内容
已知函数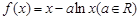 当
当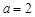 时,求曲线
时,求曲线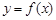 在点
在点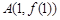 处的切线方程;求函数
处的切线方程;求函数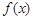 的极值
的极值
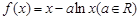 当
当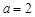 时,求曲线
时,求曲线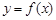 在点
在点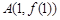 处的切线方程;求函数
处的切线方程;求函数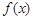 的极值
的极值当 时,函数
时,函数 无极值
无极值
当 时,函数
时,函数 在
在 处取得极小值
处取得极小值 ,无极大值
,无极大值
 时,函数
时,函数 无极值
无极值当
 时,函数
时,函数 在
在 处取得极小值
处取得极小值 ,无极大值
,无极大值函数 的定义域为
的定义域为 ,
, .
.
(Ⅰ)当 时,
时, ,
, ,
, ,
,
 在点
在点 处的切线方程为
处的切线方程为 ,即
,即 .
.
(Ⅱ)由 可知:
可知:
①当 时,
时, ,函数
,函数 为
为 上的增函数,函数
上的增函数,函数 无极值;
无极值;
②当 时,由
时,由 ,解得
,解得 ;
;
 时,
时, ,
, 时,
时,
 在
在 处取得极小值,且极小值为
处取得极小值,且极小值为 ,无极大值.
,无极大值.
综上:当 时,函数
时,函数 无极值
无极值
当 时,函数
时,函数 在
在 处取得极小值
处取得极小值 ,无极大值.
,无极大值.
此题考查的是最基本的函数切线问题及对极值含参情况的讨论,所以导数公式必需牢记,对于参数的讨论找到一个合理的分类标准做到不重不漏即可,可这往往又是学生最容易出现问题的地方。
【考点定位】 本题主要考查函数与导数、不等式的基础。注意对参数的分类讨论,属于函数中的简单题。
 的定义域为
的定义域为 ,
, .
.(Ⅰ)当
 时,
时, ,
, ,
, ,
, 在点
在点 处的切线方程为
处的切线方程为 ,即
,即 .
.(Ⅱ)由
 可知:
可知:①当
 时,
时, ,函数
,函数 为
为 上的增函数,函数
上的增函数,函数 无极值;
无极值;②当
 时,由
时,由 ,解得
,解得 ;
; 时,
时, ,
, 时,
时,
 在
在 处取得极小值,且极小值为
处取得极小值,且极小值为 ,无极大值.
,无极大值.综上:当
 时,函数
时,函数 无极值
无极值当
 时,函数
时,函数 在
在 处取得极小值
处取得极小值 ,无极大值.
,无极大值.此题考查的是最基本的函数切线问题及对极值含参情况的讨论,所以导数公式必需牢记,对于参数的讨论找到一个合理的分类标准做到不重不漏即可,可这往往又是学生最容易出现问题的地方。
【考点定位】 本题主要考查函数与导数、不等式的基础。注意对参数的分类讨论,属于函数中的简单题。

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
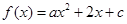 (
(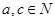 )满足①
)满足①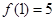 ;②
;②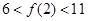
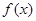 的解析式;
的解析式;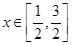 ,都有
,都有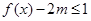 成立,求实数
成立,求实数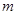 的取值范围.
的取值范围.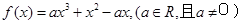
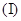 若函数
若函数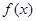 在
在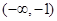 和
和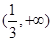 上是增函数,在
上是增函数,在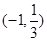 是减函数,求
是减函数,求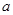 的值;
的值; 讨论函数
讨论函数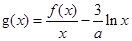 的单调递减区间;
的单调递减区间;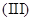 如果存在
如果存在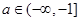 ,使函数
,使函数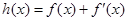 ,
,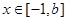
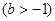 ,在
,在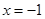 处取得最小值,试求
处取得最小值,试求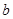 的最大值.
的最大值.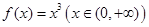
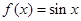
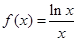
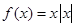
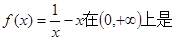 ( )
( ) 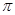 且在
且在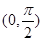 上为增函数的是( )
上为增函数的是( )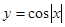
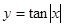
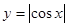
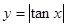
 的定义域为
的定义域为 ,若
,若 ,则实数m的范围是_______.
,则实数m的范围是_______.