题目内容

【题目】数列{an}的前n项和是Sn ， 且Sn+ =1．
（1）求数列{an}的通项公式；
（2）记bn=log3 ，数列 的前n项和为Tn ， 若不等式Tn＜m，对任意的正整数n恒成立，求m的取值范围．

【答案】
（1）解：由 ①

②

①﹣②可得 ，

∴ ，

当n=1时 ，则 ，

∴数列{an}是以 为首项， 为公比的等比数列，

因此


（2）解： ，

∴ ， ．

∵不等式Tn＜m，对任意的正整数n恒成立，

∴


【解析】（1）由 ， ，相减可得 ，再利用等比数列的通项公式即可得出；（2）利用对数的运算性质、“裂项求和”即可得出．
【考点精析】关于本题考查的数列的前n项和，需要了解数列{an}的前n项和sn与通项an的关系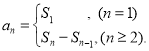才能得出正确答案．

练习册系列答案
相关题目

【题目】设：实数满足，其中；：实数满足.

（1）若，且为真，为假，求实数的取值范围；

（2）若是的充分不必要条件，求实数的取值范围.

【题目】设函数是定义域为的奇函数.

（1）求的值.

（2）若，试求不等式的解集；

（3）若在上的最小值为，求m的值.

【题目】“双十一”已经成为网民们的网购狂欢节，某电子商务平台对某市的网民在今年“双十一”的网购情况进行摸底调查，用随机抽样的方法抽取了100人，其消费金额（百元）的频率分布直方图如图所示：

（1）求网民消费金额的平均值和中位数；

（2）把下表中空格里的数填上，能否有90%的把握认为网购消费与性别有关；

【题目】已知等差数列的前项和为，等比数列的前项和为，且，，.

（1）若，求的通项公式；

（2）若，求.

【答案】（1）；（2）21或.

【解析】试题分析：（1）设等差数列公差为，等比数列公比为，由已知条件求出，再写出通项公式；（2）由，求出的值，再求出的值，求出。

试题解析：设等差数列公差为，等比数列公比为有，即.

（1）∵，结合得，

∴.

（2）∵，解得或3，

当时，，此时；

当时，，此时.

【题型】解答题
【结束】
20

【题目】如图，已知直线与抛物线相交于两点，且， 交于，且点的坐标为.

（1）求的值；

（2）若为抛物线的焦点， 为抛物线上任一点，求的最小值.

【题目】现有4个人去参加娱乐活动，该活动有甲、乙两个游戏可供参加者选择．为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏．
（1）求这4个人中恰有2人去参加甲游戏的概率；
（2）求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率；
（3）用X，Y分别表示这4个人中去参加甲、乙游戏的人数，记ξ=|X﹣Y|，求随机变量ξ的分布列与数学期望Eξ．

【题目】已知，函数.

（1）当时，解不等式；

（2）若关于的方程的解集中恰有一个元素，求的取值范围；

（3）设，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.

【题目】设函数f（x）= ，其中a＞﹣1．若f（x）在R上是增函数，则实数a的取值范围是（ ）
A.[e+1，+∞）
B.（e+1，+∞）
C.（e﹣1，+∞）
D.[e﹣1，+∞）

【题目】已知向量m＝(cos，sin )，n＝(2＋sinx，2－cos)，函数＝m·n，x∈R.

(1) 求函数的最大值；

(2) 若 且 ＝1，求的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网