��Ŀ����
����Ŀ����֪�Ȳ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ���ȱ�����
���ȱ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ��
��![]() ��
��![]() .
.
��1����![]() ����
����![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ����
����![]() .
.
���𰸡���1��![]() ����2��21��
����2��21��![]() .
.
�������������������1����Ȳ�����![]() ����Ϊ
����Ϊ![]() ���ȱ�����
���ȱ�����![]() ����Ϊ
����Ϊ![]() ������֪�������
������֪�������![]() ����д��ͨ�ʽ����2����
����д��ͨ�ʽ����2����![]() �����
�����![]() ��ֵ�������
��ֵ�������![]() ��ֵ�����
��ֵ�����![]() ��
��
�����������Ȳ�����![]() ����Ϊ
����Ϊ![]() ���ȱ�����
���ȱ�����![]() ����Ϊ
����Ϊ![]() ��
��![]() ����
����![]() .
.
��1����![]() �����
�����![]() ��
��![]() ��
��
��![]() .
.
��2����![]() �����
�����![]() ��3��
��3��
��![]() ʱ��
ʱ��![]() ����ʱ
����ʱ![]() ��
��
��![]() ʱ��
ʱ��![]() ����ʱ
����ʱ![]() .
.
�����͡������
��������
20
����Ŀ����ͼ����ֱ֪����������![]() �ཻ��
�ཻ��![]() ��������
��������![]() ��
�� ![]() ��
��![]() ��
��![]() ���ҵ�
���ҵ�![]() ������Ϊ
������Ϊ![]() .
.
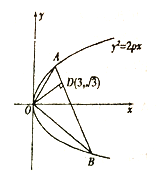
��1����![]() ��ֵ��
��ֵ��
��2����![]() Ϊ�����ߵĽ�����
Ϊ�����ߵĽ����� ![]() Ϊ����������һ������
Ϊ����������һ������![]() ����Сֵ.
����Сֵ.
���𰸡���1��![]() .��2��4.
.��2��4.
�������������������1����A��x1��y1����B��x2��y2������AB��OD��kOD=![]() ���ɵ�ֱ��AB��б��k=-
���ɵ�ֱ��AB��б��k=-![]() ���õ�ֱ��AB�ķ���Ϊ
���õ�ֱ��AB�ķ���Ϊ![]() ���������߷���������Ϊ
���������߷���������Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ����
����![]() �����ɽ��
�����ɽ��![]() ��ֵ��
��ֵ��
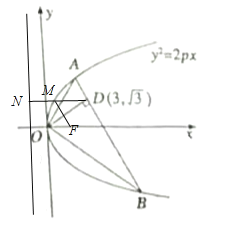
��2������M��ֱ�ߵĴ���MN������ΪN����|MF|=|MN|���������߶���֪![]() ����СֵΪ
����СֵΪ![]() �㵽������
�㵽������![]() �ߵľ���.
�ߵľ���.
���������
��1����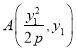 ��
�� 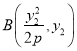 ��
�� ![]() ��
��
��![]() ��ֱ��
��ֱ��![]() �ķ���Ϊ
�ķ���Ϊ![]() ��
��
��![]() .��
.��![]() ������ʽ��
������ʽ��
������![]() ����
����![]() ����
����![]() ��
��![]() ����
����
![]() ����
����![]() ����
����![]() ����
����![]() .
.
��2������M��ֱ�ߵĴ���MN������ΪN����|MF|=|MN|���������߶���֪![]() ����СֵΪ
����СֵΪ![]() �㵽������
�㵽������![]() �ߵľ��������߷���Ϊ
�ߵľ��������߷���Ϊ![]() �����
�����![]() ����СֵΪDN=4.
����СֵΪDN=4.

����Ŀ��Ϊ�˽������ͯ�ķ����Ƿ��볣��̼�������йأ��ֶ�![]() ��Сѧ���꼶ѧ���������ʾ����飬���õ�������������ƽ��ÿ���
��Сѧ���꼶ѧ���������ʾ����飬���õ�������������ƽ��ÿ���![]() ����Ϊ�����ȡ������س���
����Ϊ�����ȡ������س���![]() Ϊ�����֡���
Ϊ�����֡���
���� | ������ | �ϼ� | |
���� | 2 | ||
������ | 18 | ||
�ϼ� | 30 |
��֪��ȫ��![]() ���������ȡ
���������ȡ![]() �ˣ��鵽���ֵ�ѧ���ĸ���Ϊ
�ˣ��鵽���ֵ�ѧ���ĸ���Ϊ![]() ��
��
��1���뽫���������������������
��2���Ƿ���![]() �İ�����Ϊ�����볣��̼�������й�?��˵��������ɣ�
�İ�����Ϊ�����볣��̼�������й�?��˵��������ɣ�
��3����֪����̼�������ҷ��ֵ�ѧ����ǡ��2��Ů�����ִӳ���̼�������ҷ��ֵ�ѧ���������ȡ2�˲μ�һ���йؽ�����ʳ�ĵ��ӽ�Ŀ����ǡ�ó鵽һ��������һ��Ů���ĸ��ʣ�
����![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
