题目内容
3. 如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路所在直线AC与DM相互垂直?
如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路所在直线AC与DM相互垂直?
分析 建立直角坐标系,求出相关点的坐标,求出直线DM的方程,然后求解M的坐标即可.
解答 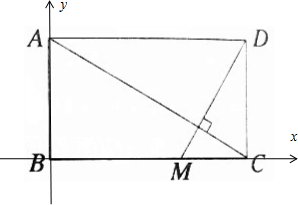 解:以B为坐标原点,BC所在直线为x轴,BA所在直线为y轴,
解:以B为坐标原点,BC所在直线为x轴,BA所在直线为y轴,
则:B(0,0),A(0,3),C(4,0),D(4,3),
kAC=$-\frac{3}{4}$,两条小路所在直线AC与DM相互垂直,可得kDM=$\frac{4}{3}$.DM所在直线方程为:y-3=$\frac{4}{3}$(x-4).
令y=0可得:x=$\frac{7}{4}$.
M所在位置距离B为:$\frac{7}{4}$m.
点评 本题考查直线方程的综合应用,直线垂直关系的应用,考查计算能力.

练习册系列答案
相关题目
13.计算:cos25°sin55°-cos65°cos55°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
14.已知A(0,-5),B(0,-1),则以线段AB为直径的圆的方程是( )
| A. | (x+3)2+y2=2 | B. | x2+(y+3)2=4 | C. | (x+3)2+y2=2 | D. | (x-3)2+y2=4 |
18.下列各值中,比tan$\frac{π}{5}$大的是( )
| A. | tan(-$\frac{π}{7}$) | B. | tan$\frac{9π}{8}$ | C. | tan35° | D. | tan(-142°) |