题目内容
已知边长为a的等边三角形内任意一点到三边距离之和为定值,这个定值为![]() ,推广到空间,棱长为a的正四面体内任意一点到各个面的距离之和也为定值,则这个定值为: .
,推广到空间,棱长为a的正四面体内任意一点到各个面的距离之和也为定值,则这个定值为: .
考点:
类比推理.
专题:
计算题;阅读型.
分析:
三角形内任意一点到三边距离和为定值是利用三角形面积相等得到的,类彼此可利用四面体的体积相等求得棱长为a的正四面体内任意一点到各个面的距离之和.
解答:
解:边长为a的等边三角形内任意一点到三边距离之和是由该三角形的面积相等得到的,
由此可以推测棱长为a的正四面体内任意一点到各个面的距离之和可由体积相等得到.
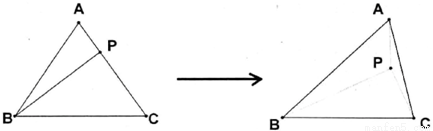
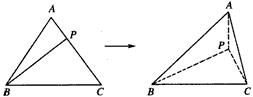
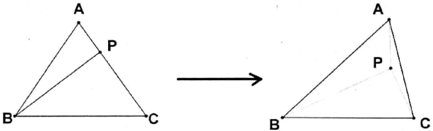
方法如下,如图,
在棱长为a的正四面体内任取一点P,P到四个面的距离分别为h1,h2,h3,h4.
四面体A﹣BCD的四个面的面积相等,均为![]() ,高为
,高为![]() .
.
由体积相等得:![]() .
.
所以![]() .
.
故答案为![]() .
.

点评:
本题考查了类比推理,考查了学生的空间想象能力,训练了等积法求点到面的距离,是基础题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,则下列命题中正确的是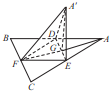 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题: