题目内容

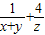已知M是△ABC内的一点（不含边界），且，若△MBC，△MCA和△MAB的面积分别为x，y，z，则的最小值是    ．
【答案】分析：利用向量的数量积公式可求，根据三角形的面积公式，可得x+y+z=1，再利用基本不等式，即可求得结论．
解答：解：∵，∠BAC=30°
∴•cos30°=
∴=4，
∴S△ABC=•sin30°=1=x+y+z
∴=（）（x+y+z）=5+
∵x＞0，y＞0，z＞0
∴≥=4
∴的最小值是9
故答案为：9
点评：本题考查向量的数量积公式，考查基本不等式的运用，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知M是△ABC内的一点，且
AB
•
AC
=2
3
，∠BAC=30°，若△MBC，△MCA和△MAB的面积分别为
1
2
，x，y，则
1
x
+
4
y
的最小值是（　　）
A、20B、18C、16D、9
已知M是△ABC内的一点（不含边界），且
AB
•
AC
=2
3
，∠BAC=30°，若△MBC，△MCA和△MAB的面积分别为x，y，z．
（1）x+y+z=
 
；
（2）定义f（x，y，z）=
1
x
+
4
y
+
9
z
，则f（x，y，z）的最小值是
 
．
已知M是△ABC内的一点，且
AB
•
AC
=2
3
，∠BAC=30°，若△MBC，△MCA，△MAB的面积分别为
1
2
，x，y，则
1
x
+
4
y
的最小值为
 
．
已知M是△ABC内的一点，且
AB
•
AC
=2
3
，∠BAC=30°．定义：f（M）=（x，y，z），其中x，y，z分别为△MBC，△MCA，△MAB的面积，若f（M）=（x，y，
1
2
），则
1
2x
+
2
y
的最小值为
9
9
，此时f（M）=（
(
1
6
，
1
3
，
1
2
)
(
1
6
，
1
3
，
1
2
)
．
已知M是△ABC内的一点（不含边界），且
AB
.
AC
=2
3
∠BAC=30°，若△MBC，△MCA和△MAB的面积分别为x，y，z，则
1
x+y
+
4
z
的最小值是
9
9
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网