题目内容
已知M是△ABC内的一点（不含边界），且| AB |
| AC |
| 3 |
（1）x+y+z=
（2）定义f（x，y，z）=
| 1 |
| x |
| 4 |
| y |
| 9 |
| z |
分析：（1）先根据向量数量积的定义求出AB•AC，从而求出△ABC的面积，而△MBC，△MCA和△MAB的面积和即为△ABC的面积，即可求出所求；
（2）先在等式f（x，y，z）=
+
+
两边同乘以x+y+z，然后利用均值不等式进行求解即可．
（2）先在等式f（x，y，z）=
| 1 |
| x |
| 4 |
| y |
| 9 |
| z |
解答：解：（1）
•
=2
=AB•AC•cos30°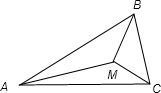
∴AB•AC=4，S△ABC=
AB•AC•sin30°=1=x+y+z
（2）∵1=x+y+z
∴f（x，y，z）=
+
+
=（
+
+
）（x+y+z）
=1+4+9+
+
+
+
+
+
≥14+4+6+12=36，
故答案为：1，36
| AB |
| AC |
| 3 |
∴AB•AC=4，S△ABC=
| 1 |
| 2 |
（2）∵1=x+y+z
∴f（x，y，z）=
| 1 |
| x |
| 4 |
| y |
| 9 |
| z |
| 1 |
| x |
| 4 |
| y |
| 9 |
| z |
=1+4+9+
| y |
| x |
| 4x |
| y |
| z |
| x |
| 9x |
| z |
| 4z |
| y |
| 9y |
| z |
≥14+4+6+12=36，
故答案为：1，36
点评：本题主要考查了向量的应用，以及三角形的面积公式，同时考查了均值不等式的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目