题目内容
10.在${({x-\frac{1}{x}-1})^4}$的展开式中,常数项为-5.分析 ${({x-\frac{1}{x}-1})^4}$的展开式中的通项公式:Tr+1=${∁}_{4}^{r}$(-1)4-r$(x-\frac{1}{x})^{r}$(r=0,1,2,3,4).$(x-\frac{1}{x})^{r}$的通项公式:Tk+1=${∁}_{r}^{k}$${x}^{r-k}(-\frac{1}{x})^{k}$=(-1)k${∁}_{r}^{k}$xr-2k,令r-2k=0,即r=2k.进而得出.
解答 解:${({x-\frac{1}{x}-1})^4}$的展开式中的通项公式:Tr+1=${∁}_{4}^{r}$(-1)4-r$(x-\frac{1}{x})^{r}$(r=0,1,2,3,4).
∵$(x-\frac{1}{x})^{r}$的通项公式:Tk+1=${∁}_{r}^{k}$${x}^{r-k}(-\frac{1}{x})^{k}$=(-1)k${∁}_{r}^{k}$xr-2k,
令r-2k=0,即r=2k.
r=0,k=0;r=2,k=1;r=4,k=2.
∴常数项=1-${∁}_{2}^{1}$×${∁}_{4}^{2}$+${∁}_{4}^{2}$×1=-5.
故答案为:-5.
点评 本题考查了二项式定理的应用、分类讨论方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
20.某几何体的三视图如图所示,则该几何体的表面积为( )
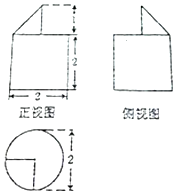

| A. | 6π+1 | B. | $\frac{{({24+\sqrt{2}})π}}{4}+1$ | C. | $\frac{{({23+\sqrt{2}})π}}{4}+\frac{1}{2}$ | D. | $\frac{{({23+\sqrt{2}})π}}{4}+1$ |
5.已知A=[1,+∞),$B=\left\{{x∈R|\frac{1}{2}≤x≤2a-1}\right\}$,若A∩B≠∅,则实数a的取值范围是( )
| A. | [1,+∞) | B. | $[{\frac{1}{2},1}]$ | C. | $[{\frac{2}{3},+∞})$ | D. | (1,+∞) |
15.若函数$f(x)=\frac{1}{2}cos2x+3a(sinx-cosx)+(4a-1)x$在$[-\frac{π}{2},0]$上单调递增,则实数a的取值范围为( )
| A. | $[\frac{1}{7},1]$ | B. | $[-1,\frac{1}{7}]$ | C. | $(-∞,-\frac{1}{7}]∪[1,+∞)$ | D. | [1,+∞) |
2.已知双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$右焦点为F,P为双曲线左支上一点,点$A(0,\sqrt{2})$,则△APF周长的最小值为4(1+$\sqrt{2}$).
19.已知抛物线y2=4x的焦点为F,过焦点F的直线交抛物线于A、B两点,O为坐标原点,若|AB|=6,则△AOB的面积为( )
| A. | $\sqrt{6}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 4 |