题目内容
 已知椭圆E的右焦点F(1,0),右准线l:x=4,离心率e=
已知椭圆E的右焦点F(1,0),右准线l:x=4,离心率e=| 1 | 2 |
(1)求椭圆E的方程;
(2)设A是椭圆E的左顶点,一经过右焦点F的直线与椭圆E相交于P、Q两点(P、Q与A不重合),直线AP、AQ分别与右准线l相交于点M、N,求证:直线PN、直线QM与x轴相交于同一点.
分析:(1)设椭圆E的标准方程为
+
=1(a>b>0).由题意可得c=1,利用离心率公式e=
及a2=b2+c2,即可.
(2)设P(x1,y1),Q(x2,y2),由于直线l的斜率不为0,可设直线l的方程为my=x-1,与椭圆方程联立得到根与系数的关系.利用点斜式分别写出直线AP、AQ的方程即可得出点M,N的坐标.只要证明kBM-kQB为0,即可得到三点Q,B,M共线,即直线QM与x轴相交于右顶点B.同理直线PN与x轴相交于右顶点B,所以直线PN、直线QM与x轴相交于同一点B.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
(2)设P(x1,y1),Q(x2,y2),由于直线l的斜率不为0,可设直线l的方程为my=x-1,与椭圆方程联立得到根与系数的关系.利用点斜式分别写出直线AP、AQ的方程即可得出点M,N的坐标.只要证明kBM-kQB为0,即可得到三点Q,B,M共线,即直线QM与x轴相交于右顶点B.同理直线PN与x轴相交于右顶点B,所以直线PN、直线QM与x轴相交于同一点B.
解答:解:(1)设椭圆E的标准方程为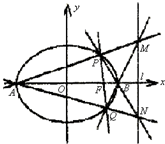
+
=1(a>b>0).
由题意可得
,解得
.
∴椭圆E的标准方程为
+
=1.
(2)设P(x1,y1),Q(x2,y2),
由于直线l的斜率不为0,可设直线l的方程为my=x-1.
联立
.消去x得到(3m2+4)y2+6my-9=0.
∴y1+y2=
,y1y2=
.
直线AP的方程为y=
(x+2),令x=4,得到y=
,∴M(4,
).
直线AQ的方程为:y=
(x+2),令x=4,得到y=
,∴N(4,
).
∴kBM-kQB=
-
=
-
=
,
其分子=3y1(my2+1-2)-y2(my1+1+2)=2my1y2-3(y1+y2)=
-
=0,
∴kBM-kQB=0,即kBM=kQB,
∴三点Q,B,M共线,即直线QM与x轴相交于右顶点B.
同理直线PN与x轴相交于右顶点B,所以直线PN、直线QM与x轴相交于同一点B.

| x2 |
| a2 |
| y2 |
| b2 |
由题意可得
|
|
∴椭圆E的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设P(x1,y1),Q(x2,y2),
由于直线l的斜率不为0,可设直线l的方程为my=x-1.
联立
|
∴y1+y2=
| -6m |
| 3m2+4 |
| -9 |
| 3m2+4 |
直线AP的方程为y=
| y1 |
| x1+2 |
| 6y1 |
| x1+2 |
| 6y1 |
| x1+2 |
直线AQ的方程为:y=
| y2 |
| x2+2 |
| 6y2 |
| x2+2 |
| 6y2 |
| x2+2 |
∴kBM-kQB=
| ||
| 4-2 |
| y2 |
| x2-2 |
| 3y1 |
| x1+2 |
| y2 |
| x2-2 |
| 3y1(x2-2)-y2(x1+2) |
| (x1+2)(x2-2) |
其分子=3y1(my2+1-2)-y2(my1+1+2)=2my1y2-3(y1+y2)=
| -18m |
| 3m2+4 |
| -18m |
| 3m2+4 |
∴kBM-kQB=0,即kBM=kQB,
∴三点Q,B,M共线,即直线QM与x轴相交于右顶点B.
同理直线PN与x轴相交于右顶点B,所以直线PN、直线QM与x轴相交于同一点B.
点评:本题中考查了椭圆的方程及其性质、直线与椭圆相交问题转化为一元二次方程的根与系数的关系、利用斜率相等证明三点共线等基础知识与基本技能,考查了分析问题和解决问题的能力、推理能力和计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
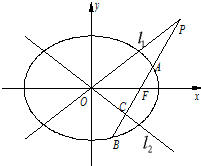 已知椭圆E的方程为
已知椭圆E的方程为 已知椭圆
已知椭圆 的半径等于椭圆E:
的半径等于椭圆E: (a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x-
(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x- 的距离为
的距离为 -
- ,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
 .
.