题目内容
已知函数f(x)=(ax2+bx+c)ex且f(0)=1,f(1)=0.
(1)若f(x)在区间[0,1]上单调递减,求实数a的取值范围;
(2)当a=0时,是否存在实数m使不等式2f(x)+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立?若存在,求出m的值,若不存在,请说明理由.
(1)若f(x)在区间[0,1]上单调递减,求实数a的取值范围;
(2)当a=0时,是否存在实数m使不等式2f(x)+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立?若存在,求出m的值,若不存在,请说明理由.
(1)[0,1](2)存在m=4,
∵f(0)=1,∴f(0)=c·e0=c=1,
又f(1)=(a+b+1)·e1=0,∴a+b+1=0,
∴b=-1-a,∴f(x)=[ax2-(1+a)x+1]·ex.
∴f′(x)=[ax2+(a-1)x-a]ex.
(1)∵函数f(x)在区间[0,1]上单调递减,∴对任意x∈[0,1],有f′(x)≤0,即对任意x∈[0,1],有ax2+(a-1)x-a≤0,令g(x)=ax2+(a-1)x-a.当a>0时,因为二次函数g(x)=ax2+(a-1)x-a的图象开口向上,而g(0)=-a<0,所以需g(1)=a-1≤0,即0<a≤1,当a=0时,对任意x∈[0,1],g(x)=-x≤0成立,符合条件,当a<0时,因为g(0)=-a>0,不符合条件.
故a的取值范围是[0,1].
(2)当a=0时,f(x)=(1-x)ex,假设存在实数m,使不等式2f(x)+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立.
由mx+1≥-x2+4x+1,得x2+(m-4)x≥0对x∈R恒成立.
∴Δ=(m-4)2≤0,∴m=4.
下面证明:当m=4时,2f(x)+4xex≥mx+1对x∈R恒成立.
即(2x+2)ex-4x-1≥0,对x∈R恒成立.
令g(x)=(2x+2)ex-4x-1,g′(x)=(2x+4)ex-4
∵g′(0)=0.
当x>0时,(2x+4)>4,ex>1,∴(2x+4)ex>4,g′(x)>0,∴g(x)在(0,+∞)上单调递增.
当x<0时,(2x+4)<4,0<ex<1,
∴(2x+4)ex<4ex<4,g′(x)<0,
∴g(x)在(-∞,0)上单调递减.
∴g(x)min=g(0)=2-1=1>0,
∴g(x)>0,即(2x+2)ex>4x+1对x∈R恒成立,
∴存在m=4,使2f(x)+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立
又f(1)=(a+b+1)·e1=0,∴a+b+1=0,
∴b=-1-a,∴f(x)=[ax2-(1+a)x+1]·ex.
∴f′(x)=[ax2+(a-1)x-a]ex.
(1)∵函数f(x)在区间[0,1]上单调递减,∴对任意x∈[0,1],有f′(x)≤0,即对任意x∈[0,1],有ax2+(a-1)x-a≤0,令g(x)=ax2+(a-1)x-a.当a>0时,因为二次函数g(x)=ax2+(a-1)x-a的图象开口向上,而g(0)=-a<0,所以需g(1)=a-1≤0,即0<a≤1,当a=0时,对任意x∈[0,1],g(x)=-x≤0成立,符合条件,当a<0时,因为g(0)=-a>0,不符合条件.
故a的取值范围是[0,1].
(2)当a=0时,f(x)=(1-x)ex,假设存在实数m,使不等式2f(x)+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立.
由mx+1≥-x2+4x+1,得x2+(m-4)x≥0对x∈R恒成立.
∴Δ=(m-4)2≤0,∴m=4.
下面证明:当m=4时,2f(x)+4xex≥mx+1对x∈R恒成立.
即(2x+2)ex-4x-1≥0,对x∈R恒成立.
令g(x)=(2x+2)ex-4x-1,g′(x)=(2x+4)ex-4
∵g′(0)=0.
当x>0时,(2x+4)>4,ex>1,∴(2x+4)ex>4,g′(x)>0,∴g(x)在(0,+∞)上单调递增.
当x<0时,(2x+4)<4,0<ex<1,
∴(2x+4)ex<4ex<4,g′(x)<0,
∴g(x)在(-∞,0)上单调递减.
∴g(x)min=g(0)=2-1=1>0,
∴g(x)>0,即(2x+2)ex>4x+1对x∈R恒成立,
∴存在m=4,使2f(x)+4xex≥mx+1≥-x2+4x+1对任意x∈R恒成立

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
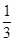 x3+
x3+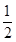 ax2+bx.
ax2+bx.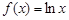 ,
,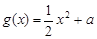 (
(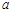 为常数),直线
为常数),直线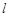 与函数
与函数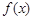 、
、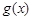 的图象都相切,且
的图象都相切,且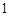 .
.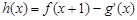 [注:
[注: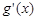 是
是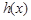 的单调递增区间;
的单调递增区间;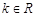 时,试讨论方程
时,试讨论方程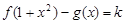 的解的个数.
的解的个数.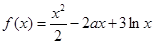
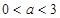 .
.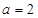 时,求函数
时,求函数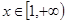 时,若
时,若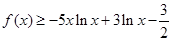 恒成立,求
恒成立,求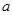 的取值范围.
的取值范围.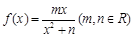 , 在
, 在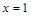 处取得极小值2.
处取得极小值2.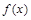 的解析式;
的解析式;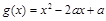 , 若对于任意
, 若对于任意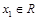 ,总存在
,总存在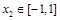 , 使得
, 使得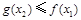 , 求实数
, 求实数 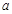 的取值范围.
的取值范围.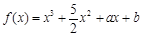 (
(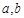 为常数),其图象是曲线
为常数),其图象是曲线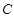 .
.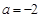 时,求函数
时,求函数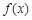 的单调减区间;
的单调减区间;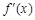 ,若存在唯一的实数
,若存在唯一的实数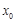 ,使得
,使得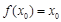 与
与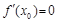 同时成立,求实数
同时成立,求实数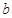 的取值范围;
的取值范围;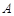 为曲线
为曲线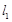 与曲线
与曲线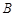 ,在点
,在点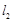 ,设切线
,设切线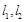 的斜率分别为
的斜率分别为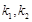 .问:是否存在常数
.问:是否存在常数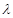 ,使得
,使得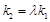 ?若存在,求出
?若存在,求出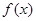 满足:
满足: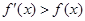 恒成立,若
恒成立,若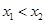 ,则
,则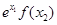 与
与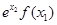 的大小关系为 ( )
的大小关系为 ( )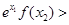
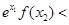
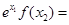
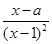 ,x∈(1,+∞).
,x∈(1,+∞).