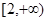题目内容
已知函数f(x)=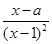 ,x∈(1,+∞).
,x∈(1,+∞).
(1)求函数f(x)的单调区间;
(2)函数f(x)在区间[2,+∞)上是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
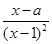 ,x∈(1,+∞).
,x∈(1,+∞).(1)求函数f(x)的单调区间;
(2)函数f(x)在区间[2,+∞)上是否存在最小值,若存在,求出最小值,若不存在,请说明理由.
(1)a≤1时,f(x)的减区间为(1,+∞);a>1时,f(x)的增区间为(1,2a-1),f(x)的减区间为(2a-1,+∞).(2)当a≥2时,f(x)有最小值2-a;当a<2时,f(x)没有最小值.
(1)f′(x)= ,x∈(1,+∞).
,x∈(1,+∞).
由f′(x)=0,得x1=1,或x2=2a-1.
①当2a-1≤1,即a≤1时,在(1,+∞)上,f′(x)<0,f(x)单调递减;
②当2a-1>1,即a>1时,在(1,2a-1)上,f′(x)>0,f(x)单调递增,在(2a-1,+∞)上,f′(x)<0,f(x)单调递减.
综上所述,a≤1时,f(x)的减区间为(1,+∞);a>1时,f(x)的增区间为(1,2a-1),f(x)的减区间为(2a-1,+∞).
(2)①当a≤1时,由(1)知f(x)在[2,+∞)上单调递减,不存在最小值;
②当a>1时,若2a-1≤2,即a≤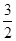 时,f(x)在[2,+∞)上单调递减,不存在最小值;
时,f(x)在[2,+∞)上单调递减,不存在最小值;
若2a-1>2,即a>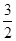 时,f(x)在[2,2a-1)上单调递增,在(2a-1,+∞)上单调递减,因为f(2a-1)=
时,f(x)在[2,2a-1)上单调递增,在(2a-1,+∞)上单调递减,因为f(2a-1)=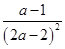 >0,且当x>2a-1时,x-a>a-1>0,所以当x≥2a-1时,f(x)>0.又因为f(2)=2-a,所以当2-a≤0,即a≥2时,f(x)有最小值2-a;当2-a>0,即
>0,且当x>2a-1时,x-a>a-1>0,所以当x≥2a-1时,f(x)>0.又因为f(2)=2-a,所以当2-a≤0,即a≥2时,f(x)有最小值2-a;当2-a>0,即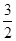 <a<2时,f(x)没有最小值.
<a<2时,f(x)没有最小值.
综上所述:当a≥2时,f(x)有最小值2-a;当a<2时,f(x)没有最小值.
 ,x∈(1,+∞).
,x∈(1,+∞).由f′(x)=0,得x1=1,或x2=2a-1.
①当2a-1≤1,即a≤1时,在(1,+∞)上,f′(x)<0,f(x)单调递减;
②当2a-1>1,即a>1时,在(1,2a-1)上,f′(x)>0,f(x)单调递增,在(2a-1,+∞)上,f′(x)<0,f(x)单调递减.
综上所述,a≤1时,f(x)的减区间为(1,+∞);a>1时,f(x)的增区间为(1,2a-1),f(x)的减区间为(2a-1,+∞).
(2)①当a≤1时,由(1)知f(x)在[2,+∞)上单调递减,不存在最小值;
②当a>1时,若2a-1≤2,即a≤
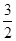 时,f(x)在[2,+∞)上单调递减,不存在最小值;
时,f(x)在[2,+∞)上单调递减,不存在最小值;若2a-1>2,即a>
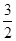 时,f(x)在[2,2a-1)上单调递增,在(2a-1,+∞)上单调递减,因为f(2a-1)=
时,f(x)在[2,2a-1)上单调递增,在(2a-1,+∞)上单调递减,因为f(2a-1)=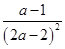 >0,且当x>2a-1时,x-a>a-1>0,所以当x≥2a-1时,f(x)>0.又因为f(2)=2-a,所以当2-a≤0,即a≥2时,f(x)有最小值2-a;当2-a>0,即
>0,且当x>2a-1时,x-a>a-1>0,所以当x≥2a-1时,f(x)>0.又因为f(2)=2-a,所以当2-a≤0,即a≥2时,f(x)有最小值2-a;当2-a>0,即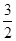 <a<2时,f(x)没有最小值.
<a<2时,f(x)没有最小值.综上所述:当a≥2时,f(x)有最小值2-a;当a<2时,f(x)没有最小值.

练习册系列答案
相关题目
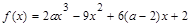 ,
,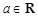 .
.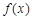 在
在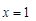 处取得极值,求实数
处取得极值,求实数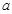 的值;
的值;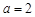 ,求函数
,求函数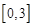 上的最大值和最小值.
上的最大值和最小值.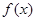 是二次函数,不等式
是二次函数,不等式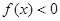 的解集是
的解集是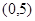 ,且
,且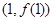 处的切线与直线
处的切线与直线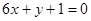 平行.
平行.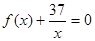 在区间
在区间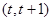 内有两个不等的实数根?
内有两个不等的实数根?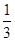 ax3-
ax3- x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.
x2+cx+d(a,c,d∈R)满足f(0)=0,f′(1)=0,且f′(x)≥0在R上恒成立.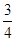 x2-bx+
x2-bx+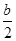 -
-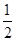 x2+bln (x+2)在(-1,+∞)上是减函数,则b的取值范围是________.
x2+bln (x+2)在(-1,+∞)上是减函数,则b的取值范围是________.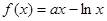 在
在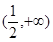 内单调递增,则
内单调递增,则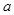 的取值范围为( )
的取值范围为( )