题目内容
已知两个非零向量为 .解关于x的不等式
.解关于x的不等式 >1(其中a>0).
>1(其中a>0).
【答案】分析:由不等式 >1可得
>1可得 >0,分a=2、0<a<2、a>2 三种情况求出不等式的解集.
>0,分a=2、0<a<2、a>2 三种情况求出不等式的解集.
解答:解:由 =
= +
+ >1,可得
>1,可得  >0.
>0.
①当a=2时,原不等式等价于 >0,∴x>2.
>0,∴x>2.
②当 0<a<2时,不等式即 <0,∴2<x<
<0,∴2<x< .
.
③当a>2时,原不等式等价于 >0,∴x>2,或 x<
>0,∴x>2,或 x< .
.
综上,当a=2时,解集为(2,+∞); ②当 0<a<2时,解集为(2, );
);
当a>2时,解集为(2,+∞)∪(-∞, ).
).
点评:本题主要考查两个向量的数量积公式,分式不等式的解法,体现了分类讨论的数学思想.
 >1可得
>1可得 >0,分a=2、0<a<2、a>2 三种情况求出不等式的解集.
>0,分a=2、0<a<2、a>2 三种情况求出不等式的解集.解答:解:由
 =
= +
+ >1,可得
>1,可得  >0.
>0.①当a=2时,原不等式等价于
 >0,∴x>2.
>0,∴x>2.②当 0<a<2时,不等式即
 <0,∴2<x<
<0,∴2<x< .
.③当a>2时,原不等式等价于
 >0,∴x>2,或 x<
>0,∴x>2,或 x< .
.综上,当a=2时,解集为(2,+∞); ②当 0<a<2时,解集为(2,
 );
);当a>2时,解集为(2,+∞)∪(-∞,
 ).
).点评:本题主要考查两个向量的数量积公式,分式不等式的解法,体现了分类讨论的数学思想.

练习册系列答案
相关题目
 .解关于x的不等式
.解关于x的不等式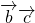 >1(其中a>0).
>1(其中a>0).