题目内容
已知点P是线段AB上的动点(不包括两端点),点O是线段AB所在直线外一点,若 =x
=x +2y
+2y (x,y∈R),则
(x,y∈R),则 的最小值是( )
的最小值是( )A.4
B.6
C.8
D.16
【答案】分析:由题意可得  ,λ>0,化简可得
,λ>0,化简可得  =(1-λ)•
=(1-λ)• +λ
+λ ,可得 x+2y=( 1-λ)+λ=1≥2
,可得 x+2y=( 1-λ)+λ=1≥2 ,从而得到
,从而得到  ≥8,再由
≥8,再由 =
= =
= ,可得
,可得 
≥8,进而得到结论.
解答:解:∵点P是线段AB上的动点(不包括两端点),∴ ,1>λ>0,∴
,1>λ>0,∴ =λ(
=λ( ),
),
化简可得 =(1-λ)•
=(1-λ)• +λ
+λ ,再由
,再由  =x
=x +2y
+2y ,可得 x=1-λ>0,2y=λ>0,
,可得 x=1-λ>0,2y=λ>0,
∴x+2y=( 1-λ)+λ=1≥2 ,化简可得 xy≤
,化简可得 xy≤ ,即
,即  ≥8,当且仅当 x=2y=
≥8,当且仅当 x=2y= 时,等号成立.
时,等号成立.
再由 =
= =
= ,可得
,可得  ≥8,
≥8,
故选 C.
点评:本题主要考查平面向量基本定理及其几何意义,基本不等式的应用,属于中档题.
 ,λ>0,化简可得
,λ>0,化简可得  =(1-λ)•
=(1-λ)• +λ
+λ ,可得 x+2y=( 1-λ)+λ=1≥2
,可得 x+2y=( 1-λ)+λ=1≥2 ,从而得到
,从而得到  ≥8,再由
≥8,再由 =
= =
= ,可得
,可得 
≥8,进而得到结论.
解答:解:∵点P是线段AB上的动点(不包括两端点),∴
 ,1>λ>0,∴
,1>λ>0,∴ =λ(
=λ( ),
),化简可得
 =(1-λ)•
=(1-λ)• +λ
+λ ,再由
,再由  =x
=x +2y
+2y ,可得 x=1-λ>0,2y=λ>0,
,可得 x=1-λ>0,2y=λ>0,∴x+2y=( 1-λ)+λ=1≥2
 ,化简可得 xy≤
,化简可得 xy≤ ,即
,即  ≥8,当且仅当 x=2y=
≥8,当且仅当 x=2y= 时,等号成立.
时,等号成立.再由
 =
= =
= ,可得
,可得  ≥8,
≥8,故选 C.
点评:本题主要考查平面向量基本定理及其几何意义,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
 ,则
,则 ;
; 到直线y=
到直线y= 的到角公式为tanα=
的到角公式为tanα= ;
; =1与方程y=
=1与方程y= 表示同一条曲线.
表示同一条曲线. =x
=x +2y
+2y (x,y∈R),则
(x,y∈R),则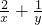 的最小值是
的最小值是