题目内容
在
中，a，b，c分别为内角A，B，C的对边，已知：
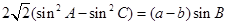，的外接圆的半径为
.
(1)求角C的大小；
(2)求的面积S的最大值.
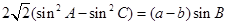中，a，b，c分别为内角A，B，C的对边，已知：，的外接圆的半径为.(1)求角C的大小；
(2)求
的面积S的最大值.(1)
；（2）
.
；（2）.试题分析：(1)先由正弦定理求出
与
的关系，再代入已知条件中，得到
，再由余弦定理得
，从而得到
；（2）由的面积
及上问得到的已知条件代入，通过三角恒等变换，得到
，再通过
的范围，得到面积S的最大值.试题解析：（1）由正弦定理有
，
，
，故有
，即有，
，又
，
.(2)由（1）可知，
，故
.又
的面积 
又因为
，故
.所以当
即
时，面积S取最大值.
练习册系列答案
名校课堂系列答案
相关题目
acos C．
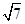，且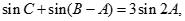
求△ABC的面积.
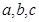分别为角A、B、C的对边，
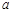=3,△ABC的面积为6，
，D为△ABC内任一点，点D到三边距离之和为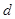
。
；
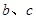中，
分别是
的对边长，已知
，求
的大小及
的值.
、
、
的对边分别为
、
、
，设S为△ABC的面积，满足
．
，且
，求
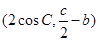，e2＝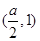
，且e1⊥e2.
，b＝
，则B＝ 
中，若
，
，
，则
的大小为_________.
中，角
所对的边分别为
，若
，则
等于 （ ）
