题目内容
是否存在实数 使得关于n的等式
使得关于n的等式
成立?若存在,求出 的值并证明等式,若不存在,请说明理由.
的值并证明等式,若不存在,请说明理由.
a=1,b=2或a=2,b=1。数学归纳法证明。
解析试题分析:假设存在满足条件的实数a,b 2分
由n=1,2等式成立解得a=1,b=2或a=2,b=1 6分
数学归纳法证明:
n=1时,左边=1,右边=1,等式成立
假设n=k时等式成立,即
当n=k+1时,左边=
8分
=
10分
= 12分
12分 时,等式成立
时,等式成立
由1,2可得 时,等式
时,等式 成立 14分
成立 14分 存在实数a,b使得等式成立. 16分
存在实数a,b使得等式成立. 16分
考点:本题主要考查数学归纳法的应用。
点评:中档题,数学归纳法的应用较为广泛,可应用于证明恒等式、整除性问题、几何问题、不等式问题,要注意“两步一结”的规范格式。本题利用n的特殊取值,确定得到a,b,再应用数学归纳法加以证明。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 =( )
=( )
A. | B. | C. | D. |
设复数 在复平面内的对应点关于虚轴对称,
在复平面内的对应点关于虚轴对称, ,则
,则 ( )
( )
A. | B.5 | C. | D. |
 ,即当
,即当 (k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*).
(k∈N*)时,an=(-1)k-1k,记Sn=a1+a2+…+an(n∈N*),用数学归纳法证明Si(2i+1)=-i(2i+1)(i∈N*). n5+
n5+ n4+
n4+ n3-
n3- n.
n. ,考查
,考查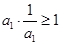 ;
; ;
; .
. 都成立的类似不等式,并用数学归纳法加以证明.
都成立的类似不等式,并用数学归纳法加以证明. 为正整数,试比较
为正整数,试比较 与
与 的大小 .
的大小 .


