题目内容
若函数 ,非零向量
,非零向量 ,我们称
,我们称 为函数
为函数 的“相伴向量”,
的“相伴向量”, 为向量
为向量 的“相伴函数”.
的“相伴函数”.
(1)已知函数 的最小正周期为
的最小正周期为 ,求函数
,求函数 的“相伴向量”;
的“相伴向量”;
(2)记向量 的“相伴函数”为
的“相伴函数”为 ,将
,将 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移 个单位长度,得到函数
个单位长度,得到函数 ,若
,若 ,求
,求 的值;
的值;
(3)对于函数 ,是否存在“相伴向量”?若存在,求出
,是否存在“相伴向量”?若存在,求出 “相伴向量”;
“相伴向量”;
若不存在,请说明理由.
 ,非零向量
,非零向量 ,我们称
,我们称 为函数
为函数 的“相伴向量”,
的“相伴向量”, 为向量
为向量 的“相伴函数”.
的“相伴函数”.(1)已知函数
 的最小正周期为
的最小正周期为 ,求函数
,求函数 的“相伴向量”;
的“相伴向量”;(2)记向量
 的“相伴函数”为
的“相伴函数”为 ,将
,将 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移 个单位长度,得到函数
个单位长度,得到函数 ,若
,若 ,求
,求 的值;
的值;(3)对于函数
 ,是否存在“相伴向量”?若存在,求出
,是否存在“相伴向量”?若存在,求出 “相伴向量”;
“相伴向量”;若不存在,请说明理由.
(1)(1,1);(2)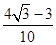 ;(3)不存在“相伴向量”
;(3)不存在“相伴向量”
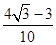 ;(3)不存在“相伴向量”
;(3)不存在“相伴向量”试题分析:(1)由函数
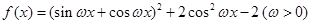 平方项展开化简,再通过化一公式即可得一个函数的形式,又因为最小正周期为
平方项展开化简,再通过化一公式即可得一个函数的形式,又因为最小正周期为 ,即可求得
,即可求得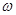 的值.再将函数展开写成
的值.再将函数展开写成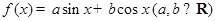 的形式及可得结论.
的形式及可得结论.(2)由向量
 为函数
为函数 的“相伴向量”,所以可得到函数
的“相伴向量”,所以可得到函数 .再将
.再将 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移 个单位长度,得到函数
个单位长度,得到函数 .再根据
.再根据 .通过解三角方程即可得到所求的结论.
.通过解三角方程即可得到所求的结论.(3)对于函数
 ,是否存在“相伴向量”.通过反证法的思想,可证明不存在函数
,是否存在“相伴向量”.通过反证法的思想,可证明不存在函数 的“相伴向量”.
的“相伴向量”.(1)
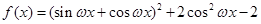

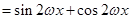
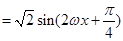 , 1分
, 1分依题意得
 ,故
,故 . 2分
. 2分∴
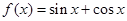 ,即
,即 的“相伴向量”为(1,1). 3分
的“相伴向量”为(1,1). 3分(2)依题意,
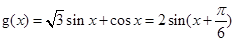 , 4分
, 4分将
 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
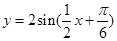 , 5分
, 5分再将所得的图象上所有点向左平移
 个单位长度,得到
个单位长度,得到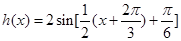 ,
,即
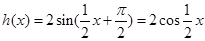 , 6分
, 6分∵
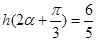 ,∴
,∴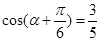 ,
,∵
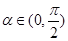 ,∴
,∴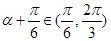 ,∴
,∴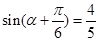 , 8分
, 8分∴
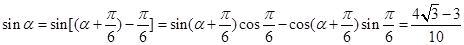 . 10分
. 10分(3)若函数
 存在“相伴向量”,
存在“相伴向量”,则存在
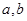 ,使得
,使得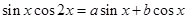 对任意的
对任意的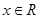 都成立, 11分
都成立, 11分令
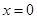 ,得
,得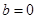 ,
,因此
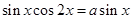 ,即
,即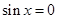 或
或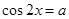 ,
,显然上式对任意的
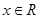 不都成立,
不都成立,所以函数
 不存在“相伴向量”. 13分
不存在“相伴向量”. 13分(注:本题若化成
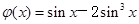 ,直接说明不存在的,给1分)
,直接说明不存在的,给1分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 图象的一部分.则
图象的一部分.则 的值为( )
的值为( )




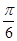 )+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为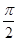 .
.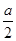 )=2,求α的值.
)=2,求α的值. 的图象,只需将函数y=sin 2x的图象( )
的图象,只需将函数y=sin 2x的图象( )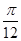 个单位
个单位 个单位
个单位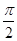 )使sin α+cos α=
)使sin α+cos α=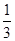 ;
;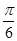 |的最小正周期为π.
|的最小正周期为π. ,使
,使 (2)存在实数
(2)存在实数
 是偶函数 (4)若
是偶函数 (4)若 是第一象限的角,且
是第一象限的角,且 ,则
,则 .其中正确命题的序号是________________________________
.其中正确命题的序号是________________________________ ,函数
,函数 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为 .
. 的值;
的值; ,
, ,求
,求 的值;
的值; ,且
,且 有且仅有一个实根,求实数
有且仅有一个实根,求实数 的值.
的值. ,
, ,函数
,函数 .
. 时,求函数
时,求函数 的取值范围;
的取值范围; ,且
,且 时,求
时,求 的值.
的值. ,则
,则 的值为 .
的值为 .