题目内容
已知向量 ,函数
,函数 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为 .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 的值;
的值;
(3)若 ,且
,且 有且仅有一个实根,求实数
有且仅有一个实根,求实数 的值.
的值.
 ,函数
,函数 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为 .
.(1)求
 的值;
的值;(2)若
 ,
, ,求
,求 的值;
的值;(3)若
 ,且
,且 有且仅有一个实根,求实数
有且仅有一个实根,求实数 的值.
的值.(1) ;(2)
;(2) ;(3)
;(3) .
.
 ;(2)
;(2) ;(3)
;(3) .
.试题分析:(1)根据数量积公式将
 进行化简,得到
进行化简,得到 ,两相邻对称轴之间的距离为半个周期,所以根据周期公式
,两相邻对称轴之间的距离为半个周期,所以根据周期公式 ,得到
,得到 的值;
的值;(2)根据第一问
 ,可得
,可得 ,所以
,所以 ,用已知角表示未知角,根据
,用已知角表示未知角,根据 的范围,求出
的范围,求出 的范围,最后求
的范围,最后求 的值;
的值;(3)画出
 ,
, 的图像,令
的图像,令 ,与其只有一个交点,即可求出
,与其只有一个交点,即可求出 的值.
的值.解:由题意,



 ,
,(1)∵两相邻对称轴间的距离为
 ,
,∴
 , ∴
, ∴ . 4分
. 4分(2)由(1)得,
 ,
,∵
 , ∴
, ∴ ,
,∴
 ,
,∴



 . 8分
. 8分(3)
 ,且余弦函数在
,且余弦函数在 上是减函数, ∴
上是减函数, ∴ ,
,令
 =
= ,
, ,在同一直角坐标系中作出两个函数的图象,可知
,在同一直角坐标系中作出两个函数的图象,可知 . 13分
. 13分
练习册系列答案
相关题目
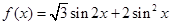 .
.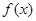 的最小正周期;
的最小正周期;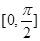 上的最大值和最小值.
上的最大值和最小值. .
. 的最小正周期;
的最小正周期; 时,求函数
时,求函数 ,非零向量
,非零向量 ,我们称
,我们称 为函数
为函数 的“相伴向量”,
的“相伴向量”, 的最小正周期为
的最小正周期为 ,求函数
,求函数 的“相伴函数”为
的“相伴函数”为 ,将
,将 个单位长度,得到函数
个单位长度,得到函数 ,若
,若 ,求
,求 的值;
的值; ,是否存在“相伴向量”?若存在,求出
,是否存在“相伴向量”?若存在,求出 “相伴向量”;
“相伴向量”; 和函数
和函数 在
在 内都是( )
内都是( ) ( )
( ) 、
、 上递增,在
上递增,在 、
、 上递减
上递减 上递增,在
上递增,在 上递减
上递减 、
、 上递增,在
上递增,在 、
、 ,若
,若 是偶函数,则
是偶函数,则 __________.
__________.

 与直线
与直线 在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则
在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则 .(
.( 表示
表示 与
与 两点间的距离).
两点间的距离).