题目内容
1.已知抛物线的顶点在原点,准线方程为x=1,F是焦点,过点A(-2,0)的直线与抛物线交于P(x1,y1),Q(x2,y2)两点,直线PF,QF分别交抛物线于点M,N.(1)求抛物线的方程及y1y2的值;
(2)记直线PQ,MN的斜率分别为k1,k2,证明:$\frac{{k}_{1}}{{k}_{2}}$为定值.
分析 (1)抛物线的顶点在原点,准线方程为x=1,可得抛物线的方程;依题意,设直线AB的方程为x=my-2,与抛物线方程联立消x得关于y的一元二次方程,根据韦达定理即可求得y1y2;
(2)设M(x3,y3),N(x4,y4),设直线AM的方程为x=ny-1,将其代入y2=-4x,消去x,得到关于y的一元二次方程,从而得y1y3=-4,同理可得 y2y4=-4,根据斜率公式可把$\frac{{k}_{1}}{{k}_{2}}$表示成关于y1与y2的表达式,再借助(1)的结果即可证明.
解答 (1)解:抛物线的顶点在原点,准线方程为x=1,∴抛物线的方程为y2=-4x,
设PQ的方程为x=my-2,代入y2=-4x,可得y2+4my-8=0
∴y1y2=-8;
(2)证明:设M(x3,y3),N(x4,y4).
则$\frac{{k}_{1}}{{k}_{2}}$=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}•\frac{{x}_{3}-{x}_{4}}{{y}_{3}-{y}_{4}}$=$\frac{{y}_{3}+{y}_{4}}{{y}_{1}+{y}_{2}}$
设直线PM的方程为x=ny-1(n≠0),将其代入y2=-4x,消去x,
整理得 y2+4ny-4=0
∴y1y3=-4.
同理可得 y2y4=-4.
故$\frac{{k}_{1}}{{k}_{2}}$=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}•\frac{{x}_{3}-{x}_{4}}{{y}_{3}-{y}_{4}}$=$\frac{{y}_{3}+{y}_{4}}{{y}_{1}+{y}_{2}}$=-$\frac{4}{{y}_{1}{y}_{2}}$.
由(1)知,y1y2=-8,
∴$\frac{{k}_{1}}{{k}_{2}}$=$\frac{1}{2}$为定值.
点评 本题考查直线与圆锥曲线的位置关系及抛物线的简单性质,考查学生综合运用知识分析问题解决问题的能力,难度较大.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{3π}{8}$ | D. | $\frac{π}{16}$ |
 ,
, ,
, ,则( )
,则( ) B.
B.
 D.
D.
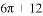 B.
B. 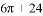 C.
C.  D.
D. 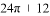
 中,角
中,角 ,
, ,
, 所对的边长分别为
所对的边长分别为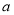 ,
,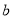 ,
,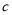 ,
,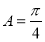 ,
,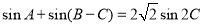 ,且△
,且△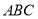 的面积为1,则
的面积为1,则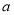 的值为( )
的值为( ) B.
B.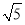 C.
C.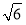 D.
D.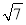

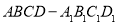 中,
中, 与
与 异面
异面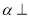 平面
平面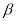 ,平面
,平面 平面
平面 ,则平面
,则平面 平面
平面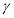
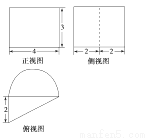
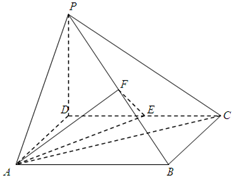 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,E、F分别为CD、PB的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD=2,E、F分别为CD、PB的中点.