题目内容

已知A、B分别是椭圆=1的右顶点和上顶点，动点C在该椭圆上运动，求△ABC的重心G的轨迹的普通方程.

思路分析：本题有两种思考方式，求解时把点C的坐标设为一般的(x1,y1)的形式或根据它在该椭圆上运动也可以设为(6cosθ,3sinθ)的形式，从而予以求解.

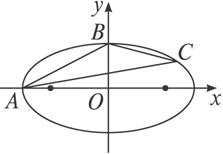
图2-2-1

解：由动点C在该椭圆上运动，故据此可设点C的坐标为(6cosθ,3sinθ).点G的坐标为(x,y)，则由题意可知点A(6，0)、B(0，3).

由重心坐标公式,可知有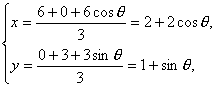

由此消去θ,得到+(y-1)2=1即为所求.

    深化升华 本题的解法体现了椭圆的参数方程对于解决相关问题的优越性.运用参数方程显得很简单，运算更简便.

练习册系列答案
相关题目
已知A、B分别是椭圆
x2
a2
+
y2
b2
=1的左右两个焦点，O为坐标原点，点P（-1，
2
2
）在椭圆上，线段PB与y轴的交点M为线段PB的中点．
（1）求椭圆的标准方程；
（2）点C是椭圆上异于长轴端点的任意一点，对于△ABC，求
sinA+sinB
sinC
的值．
已知A，B分别是椭圆C：
x2
a2
+
y2
b2
=1，(a＞b＞0)的左右顶点，F1是椭圆C的左焦点，|AF1|=2-
3
，离心率e=
3
2
．
（1）求椭圆C的方程；
（2）设P为椭圆C上异于A，B的任意一点，且PH⊥x轴，H为垂足，延长HP到点Q使得|HP|=|PQ|，连接AQ，并延长AQ交直线l：x=2于M点，N为MB中点，求
OQ
•
QN
的值，并判断以O为圆心，OQ为半径的圆与直线QN的位置关系．
已知A，B分别是椭圆C1：
x2
a2
+
y2
b2
=1的左、右顶点，P是椭圆上异与A，B的任意一点，Q是双曲线C2：
x2
a2
-
y2
b2
=1上异与A，B的任意一点，a＞b＞0．
（I）若P（
5
2
，
3
），Q（
5
2
，1），求椭圆Cl的方程；
（Ⅱ）记直线AP，BP，AQ，BQ的斜率分别是k1，k2，k3，k4，求证：k1•k2+k3•k4为定值；
（Ⅲ）过Q作垂直于x轴的直线l，直线AP，BP分别交 l于M，N，判断△PMN是否可能为正三角形，并说明理由．
已知A、B分别是椭圆=1的右顶点和上顶点，动点C在该椭圆上运动，求△ABC的重心G的轨迹的普通方程.

（本题14分）已知A、B分别是椭圆的左右两个焦点，O为坐标原点，点P 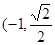）在椭圆上，线段PB与y轴的交点M为线段PB的中点。

（1）求椭圆的标准方程；

（2）点是椭圆上异于长轴端点的任一点，对于△ABC，求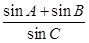的值。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网