题目内容

已知A、B分别是椭圆
x2
a2
+
y2
b2
=1的左右两个焦点，O为坐标原点，点P（-1，
2
2
）在椭圆上，线段PB与y轴的交点M为线段PB的中点．
（1）求椭圆的标准方程；
（2）点C是椭圆上异于长轴端点的任意一点，对于△ABC，求
sinA+sinB
sinC
的值．
分析：（1）由OM是△PAB的中位线得到PA⊥AB，由
c =1
1
a2
+
1
2b2
=1
a2=b2+c2
 解得a2和b2的值，从而得到椭圆的标准方程，
（2）由椭圆的定义AC+BC=2a，△ABC中，由正弦定理求得
sinA+sinB
sinC
的值．
解答：精英家教网解：（1）∵点M是线段PB的中点，∴OM是△PAB的中位线，
又OM⊥AB，∴PA⊥AB．
∴
c =1
1
a2
+
1
2b2
=1
a2=b2+c2
，解得a2=2，b2=1，c2=1，
∴椭圆的标准方程为 
x2
2
+y2=1．
（2）∵点C在椭圆上，A、B是椭圆的两个焦点，
∴AC+BC=2a=2
2
，AB=2c=2，
在△ABC中，由正弦定理，
BC
sinA
=
AC
sinB
=
AB
sinC
，
∴
sinA+sinB
sinC
=
BC+AC
AB
=
2
2
2
=
2
．
点评：本题考查椭圆的简单性质和椭圆的标准方程的应用，正弦定理的应用，属于中档题．
练习册系列答案
相关题目
已知A，B分别是椭圆C：
x2
a2
+
y2
b2
=1，(a＞b＞0)的左右顶点，F1是椭圆C的左焦点，|AF1|=2-
3
，离心率e=
3
2
．
（1）求椭圆C的方程；
（2）设P为椭圆C上异于A，B的任意一点，且PH⊥x轴，H为垂足，延长HP到点Q使得|HP|=|PQ|，连接AQ，并延长AQ交直线l：x=2于M点，N为MB中点，求
OQ
•
QN
的值，并判断以O为圆心，OQ为半径的圆与直线QN的位置关系．
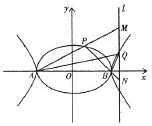已知A，B分别是椭圆C1：
x2
a2
+
y2
b2
=1的左、右顶点，P是椭圆上异与A，B的任意一点，Q是双曲线C2：
x2
a2
-
y2
b2
=1上异与A，B的任意一点，a＞b＞0．
（I）若P（
5
2
，
3
），Q（
5
2
，1），求椭圆Cl的方程；
（Ⅱ）记直线AP，BP，AQ，BQ的斜率分别是k1，k2，k3，k4，求证：k1•k2+k3•k4为定值；
（Ⅲ）过Q作垂直于x轴的直线l，直线AP，BP分别交 l于M，N，判断△PMN是否可能为正三角形，并说明理由．
已知A、B分别是椭圆=1的右顶点和上顶点，动点C在该椭圆上运动，求△ABC的重心G的轨迹的普通方程.

（本题14分）已知A、B分别是椭圆的左右两个焦点，O为坐标原点，点P 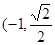）在椭圆上，线段PB与y轴的交点M为线段PB的中点。

（1）求椭圆的标准方程；

（2）点是椭圆上异于长轴端点的任一点，对于△ABC，求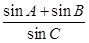的值。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网