题目内容
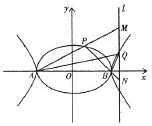 已知A,B分别是椭圆C1:
已知A,B分别是椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(I)若P(
| ||
| 2 |
| 3 |
| 5 |
| 2 |
(Ⅱ)记直线AP,BP,AQ,BQ的斜率分别是k1,k2,k3,k4,求证:k1•k2+k3•k4为定值;
(Ⅲ)过Q作垂直于x轴的直线l,直线AP,BP分别交 l于M,N,判断△PMN是否可能为正三角形,并说明理由.
分析:(Ⅰ)把点P的坐标代入椭圆方程,点Q的坐标代入双曲线方程,两式联立后可求得a2与b2的值,从而求出椭圆的方程;
(Ⅱ)设出P、Q的坐标,由两点式直接写出直线AP,BP,AQ,BQ的斜率,把P、Q的纵坐标分别用横坐标表示,代入k1•k2+k3•k4后整理即可得到结论;
(Ⅲ)假设△PMN能为正三角形,利用平面几何知识可得到∠PAN=30°,∠PBA=30°,从而得到点P位于椭圆的短轴的两个端点时△PMN能为正三角形.
(Ⅱ)设出P、Q的坐标,由两点式直接写出直线AP,BP,AQ,BQ的斜率,把P、Q的纵坐标分别用横坐标表示,代入k1•k2+k3•k4后整理即可得到结论;
(Ⅲ)假设△PMN能为正三角形,利用平面几何知识可得到∠PAN=30°,∠PBA=30°,从而得到点P位于椭圆的短轴的两个端点时△PMN能为正三角形.
解答:(Ⅰ)解:∵P(
,
)在椭圆
+
=1上,Q(
,1)在双曲线
-
=1上,
则
,
①+②×3得:
=4,a2=5,
把a2=5代入①得,b2=4.
所以椭圆Cl的方程为
+
=1;
(Ⅱ)证明:由A(-a,0),B(a,0),
设P(x1,y1),Q(x2,y2),
则k1=
,k2=
,k3=
,k4=
k1•k2+k3•k4=
•
+
•
=
+
∵设P(x1,y1)在椭圆
+
=1上,Q(x2,y2)在双曲线
-
=1上,
∴y12=
(a2-x12),y22=
(x22-a2)
则k1•k2+k3•k4=
+
=
+
=-
+
=0.
所以k1•k2+k3•k4为定值;
(Ⅲ)假设△PMN是正三角形,
∴∠MPN=∠PMN=60°,
又∵MN⊥x轴,∴∠PAN=30°,∠PBA=30°,
∴△PAB为等腰三角形,∴点P位于y轴上,且P在椭圆上,
∴点P的坐标为(0,±b),
此时
=tan30°=
=
,
即a=
b.
综上,当a=
b,且点P的坐标为(0,±b)时,△PMN为正三角形.
| ||
| 2 |
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
则
|
①+②×3得:
| 80 |
| 4a2 |
把a2=5代入①得,b2=4.
所以椭圆Cl的方程为
| x2 |
| 5 |
| y2 |
| 4 |
(Ⅱ)证明:由A(-a,0),B(a,0),
设P(x1,y1),Q(x2,y2),
则k1=
| y1 |
| x1+a |
| y1 |
| x1-a |
| y2 |
| x2+a |
| y2 |
| x2-a |
k1•k2+k3•k4=
| y1 |
| x1+a |
| y1 |
| x1-a |
| y2 |
| x2+a |
| y2 |
| x2-a |
=
| y12 |
| x12-a2 |
| y22 |
| x22-a2 |
∵设P(x1,y1)在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
∴y12=
| b2 |
| a2 |
| b2 |
| a2 |
则k1•k2+k3•k4=
| y12 |
| x12-a2 |
| y22 |
| x22-a2 |
| ||
| x12-a2 |
| ||
| x22-a2 |
| b2 |
| a2 |
| b2 |
| a2 |
所以k1•k2+k3•k4为定值;
(Ⅲ)假设△PMN是正三角形,
∴∠MPN=∠PMN=60°,
又∵MN⊥x轴,∴∠PAN=30°,∠PBA=30°,
∴△PAB为等腰三角形,∴点P位于y轴上,且P在椭圆上,
∴点P的坐标为(0,±b),
此时
| |OP| |
| |OA| |
| b |
| a |
| ||
| 3 |
即a=
| 3 |
综上,当a=
| 3 |
点评:本题是圆锥曲线的综合题,考查了利用代入法求圆锥曲线的方程,训练了学生的整体运算能力,考查了平面几何知识在圆锥曲线问题中的应用,是有一定难度题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P 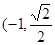 )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。 是椭圆上异于长轴端点的任一点,对于△ABC,求
是椭圆上异于长轴端点的任一点,对于△ABC,求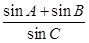 的值。
的值。