题目内容
f'(x)是f(x)的导函数,f'(x)的图象如右图所示,则f(x)的图象只可能是( )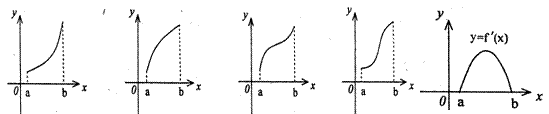
(A) (B) (C) (D)

(A) (B) (C) (D)
选D
由导数的图像可知,f(x)在[a,b]上是增函数,并且并且增速是先快后慢所以应选D

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
题目内容


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案