题目内容
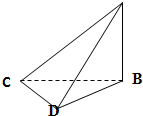
四面体ABCD中，设M是CD的中点，则
化简的结果是
- A.
- B.
- C.
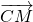
- D.
A
分析：由已知中四面体ABCD中，设M是CD的中点，可得=
，代入根据向量加法的三角形法则，可得答案．
解答：∵四面体ABCD中，M是CD的中点，
∴=
∴
=
=
故选A
点评：本题考查的知识点是向量加法及其几何意义，其中根据M是CD的中点，得到=是解答本题的关键．
分析：由已知中四面体ABCD中，设M是CD的中点，可得
=，代入根据向量加法的三角形法则，可得答案．解答：∵四面体ABCD中，M是CD的中点，
∴
=∴
=
=
故选A
点评：本题考查的知识点是向量加法及其几何意义，其中根据M是CD的中点，得到
=是解答本题的关键． 
练习册系列答案
阅读快车系列答案
相关题目
在四面体ABCD中，设AB=1，CD=2且AB⊥CD，若异面直线AB与CD间的距离为2，则四面体ABCD的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在四面体ABCD中，设AB=1，CD=
，直线AB与CD的距离为2，夹角为
，则四面体ABCD的体积等于（ ）
| 3 |
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
给出以下判断：