题目内容
已知函数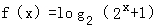 .
.
(1)用定义证明:函数f(x)在(﹣∞,+∞)内单调递增;
(2)记f﹣1(x)为函数f(x)的反函数,求函数m=f﹣1(x)﹣f(x)在[1,2]上的值域.
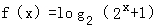 .
.(1)用定义证明:函数f(x)在(﹣∞,+∞)内单调递增;
(2)记f﹣1(x)为函数f(x)的反函数,求函数m=f﹣1(x)﹣f(x)在[1,2]上的值域.
证明:(1)任取x1<x2,则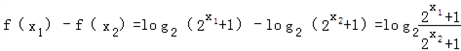 ,
,
∵x1<x2,
∴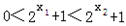 ,
,
∴ ,
,
∴f(x1)<f(x2),即函数f(x)在(﹣∞,+∞)内单调递增.
(2)∵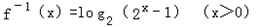 ,
,
∴m=f﹣1(x)﹣f(x)=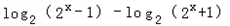
= ,
,
当1≤x≤2时,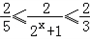 ,
,
∴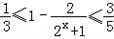 ,
,
∴m的取值范围是 .
.

练习册系列答案
相关题目
 ,
,

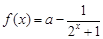 ,
,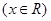 .
.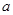 为何实数
为何实数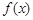 在
在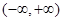 上为增函数;
上为增函数; ,
, .
. 为何实数
为何实数 在
在 上为增函数;
上为增函数;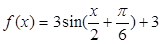 ,
,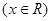

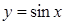 ,
, .
. 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴; (3)说明此函数图象可由
(3)说明此函数图象可由 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.