题目内容
已知函数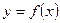 的图像经过坐标原点,且
的图像经过坐标原点,且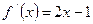 ,数列
,数列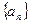 的前
的前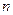 项和
项和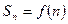
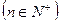
(1)求数列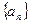 的通项公式;
的通项公式;
(2)若数列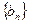 满足
满足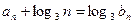 ,求数列
,求数列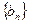 的前
的前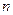 项和;
项和;
(3)若正数数列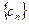 满足
满足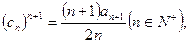 求数列
求数列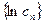 中的最大值。
中的最大值。
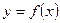 的图像经过坐标原点,且
的图像经过坐标原点,且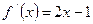 ,数列
,数列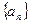 的前
的前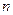 项和
项和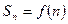
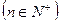
(1)求数列
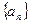 的通项公式;
的通项公式;(2)若数列
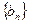 满足
满足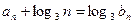 ,求数列
,求数列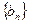 的前
的前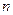 项和;
项和;(3)若正数数列
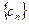 满足
满足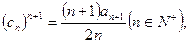 求数列
求数列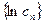 中的最大值。
中的最大值。(1)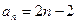
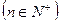 ;
;
(2)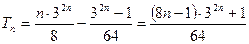 ;
;
(3)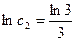
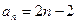
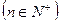 ;
;(2)
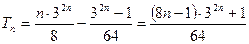 ;
;(3)
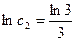
(1)由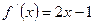 ,得
,得 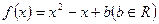
因为图像经过坐标原点,所以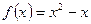 …………2分
…………2分
即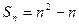
所以 当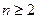 ,
,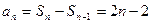
又因为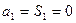 所以
所以 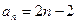
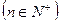 …………4分
…………4分
(2)由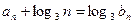 得,
得, 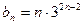
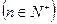 …………6分
…………6分
所以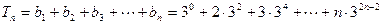 ①
①
 ②
②
②—①得,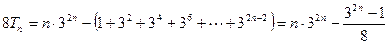
所以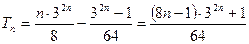 …………9分
…………9分
(3)由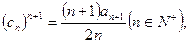 得
得 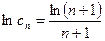 …………10分
…………10分
令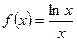 ,则
,则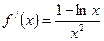 …………11分
…………11分
所以在区间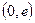 上,
上,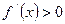 ,在区间
,在区间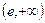 上,
上,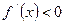
即函数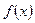 在区间
在区间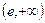 递减,故当
递减,故当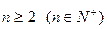 时,
时,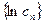 是递减数列…12分
是递减数列…12分
又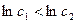 ,所以数列
,所以数列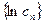 中的最大项为
中的最大项为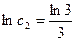 …………14分
…………14分
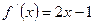 ,得
,得 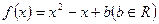
因为图像经过坐标原点,所以
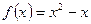 …………2分
…………2分即
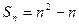
所以 当
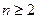 ,
,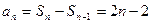
又因为
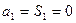 所以
所以 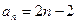
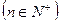 …………4分
…………4分(2)由
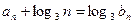 得,
得, 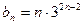
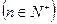 …………6分
…………6分所以
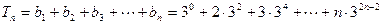 ①
① ②
②②—①得,
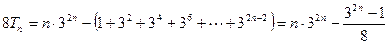
所以
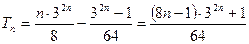 …………9分
…………9分(3)由
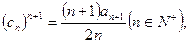 得
得 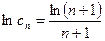 …………10分
…………10分令
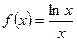 ,则
,则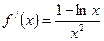 …………11分
…………11分所以在区间
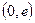 上,
上,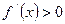 ,在区间
,在区间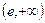 上,
上,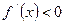
即函数
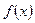 在区间
在区间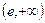 递减,故当
递减,故当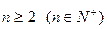 时,
时,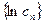 是递减数列…12分
是递减数列…12分又
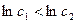 ,所以数列
,所以数列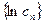 中的最大项为
中的最大项为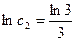 …………14分
…………14分
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
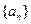 的前
的前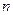 项和为
项和为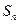 ,且
,且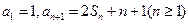 。
。 (1)求数列
(1)求数列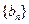 各项均为正数,满足
各项均为正数,满足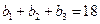 ,且
,且 ,成等比数列。证明:
,成等比数列。证明: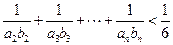 。
。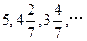 的前
的前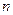 项和为
项和为 ,求使得
,求使得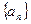 是等差数列,且
是等差数列,且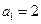 ,
,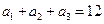 .
.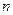 项和
项和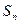 ;
;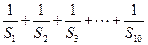 的值.
的值.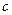 的等比数列
的等比数列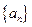 的首项
的首项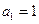 且满足
且满足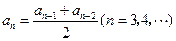 .
.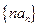 的前
的前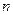 项和
项和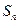 .
.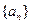 是由正数组成的比数列,
是由正数组成的比数列,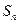 是其前
是其前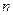 项和.
项和.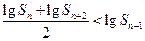 ;
;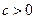 ,使得
,使得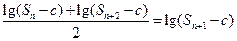 成立?并证明你的结论.
成立?并证明你的结论.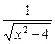 (x<-2).
(x<-2).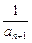 =-f--1(an)(n∈N*),求an;
=-f--1(an)(n∈N*),求an;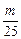 成立?若存在,求出m的值;若不存在,说明理由.
成立?若存在,求出m的值;若不存在,说明理由.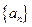 中,若
中,若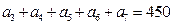 ,那么
,那么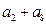 等于多少?
等于多少?