题目内容
在锐角△ABC中,角A、B、C的对边分别为a、b、c,且满足(2a-c)cos B=
bcos C.
(1)求角B的大小;
(2)设m=(sin A,1),n=(3,cos 2A),试求m·n的取值范围.
解 (1)因为(2a-c)cos B=bc os C,
os C,
所以(2sin A-sin C)cos B=sin Bcos C,
即2sin Acos B=sin Ccos B+sin Bcos C
=sin(C+B)=sin A.
而sin A>0,所以cos B= .
.
又∵0°<B<180°,∴B=60°.
(2)因为m=(sin A,1),n=(3,cos 2A),
所以m·n=3sin A+cos 2A=3sin A+1-2sin2A
 由
由 所以30°<A<90°,从而sin A∈
所以30°<A<90°,从而sin A∈ ,
,
故m·n的取值范围是 .
.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 ,
, ,
, ,则执行如图所示的程序框图,输出的
,则执行如图所示的程序框图,输出的 值( )
值( )

 B.
B.  C.
C. D.
D.
 是“直线
是“直线 与圆
与圆 相交”的
相交”的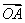 =(1,2),
=(1,2), =(4,1),
=(4,1), =(0,-1),则△ABC的形状是______________.
=(0,-1),则△ABC的形状是______________. ·
·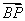 ·
·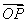 ·
·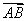 的最小值为________.
的最小值为________. 的单位向量,且向量a=2e1+e2,向量b=-3e1+2e2,则a·b=______.
的单位向量,且向量a=2e1+e2,向量b=-3e1+2e2,则a·b=______. 错误命题的序号为____________.
错误命题的序号为____________. ,
, =________.
=________.