题目内容
设椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 、
、 ,上顶点为
,上顶点为 ,在
,在 轴负半轴上有一点
轴负半轴上有一点 ,满足
,满足 ,且
,且 ⊥
⊥ .
.

(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(Ⅲ)在(Ⅱ)的条件下,过右焦点 作斜率为
作斜率为 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、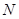 两点,
两点,
若点 使得以
使得以 为邻边的平行四边形是菱形,求
为邻边的平行四边形是菱形,求 的取值范围.
的取值范围.
【答案】
解:(Ⅰ)由题意知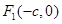 ,
,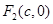 ,
,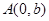
∵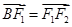 知
知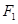 为
为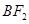 的中点,
的中点,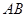 ⊥
⊥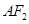
∴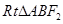 中,
中,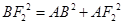
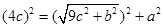 ,又
,又
∴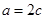
故椭圆的离心率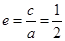 ……………………………………………3分
……………………………………………3分
(Ⅱ)由(Ⅰ)知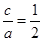 得
得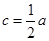 ,于是
,于是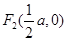 ,
, 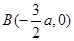 ,
,
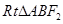 的外接圆圆心为(
的外接圆圆心为(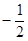
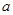 ,0),半径
,0),半径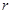 =
=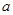 ,
,
所以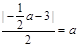 ,解得
,解得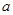 =2,∴
=2,∴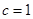 ,
,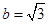 ,
,
所求椭圆方程为 ………………………………………6分
………………………………………6分
(Ⅲ)由(Ⅱ)知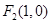 ,
,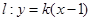 ,设
,设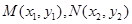 ,
,
由 代入得
代入得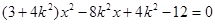
则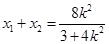 ,
,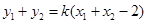 ………………………8分
………………………8分

由于菱形对角线垂直,则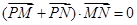
故
即
 ……………………………10分
……………………………10分
由已知条件知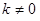
∴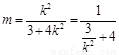
∴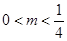 故
故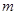 的取值范围是
的取值范围是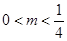 .……12分
.……12分
【解析】略

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 :
: 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,过点
,过点 垂直的直线交
垂直的直线交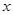 轴负半轴于点
轴负半轴于点 ,且
,且 .
. 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切,
相切, :
:
 的左、右焦点分别为
的左、右焦点分别为
 ,过点
,过点 垂直的直线交
垂直的直线交 轴负半轴于点
轴负半轴于点 ,且
,且 ,若过
,若过 三点的圆恰好与直线
三点的圆恰好与直线 :
: 相切. 过定点
相切. 过定点 的直线
的直线 与椭圆
与椭圆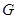 ,
, 两点(点
两点(点 ,
,
 ,在
,在 ,使得以
,使得以 ,
, 为邻边的平行四边形是菱形. 如果存在,求出
为邻边的平行四边形是菱形. 如果存在,求出 的取值范围,如果不存在,请说明理由;
的取值范围,如果不存在,请说明理由; 满足
满足 ,求
,求 的取值范围.
的取值范围. :
: 的左、右焦点分别是
的左、右焦点分别是 ,下顶点为
,下顶点为 ,线段
,线段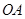 的中点为
的中点为 (
( 为坐标原点),如图.若抛物线
为坐标原点),如图.若抛物线 :
: 与
与 轴的交点为
轴的交点为 ,
, 为抛物线
为抛物线 两点,求
两点,求 面积的最大值.
面积的最大值.