题目内容
已知二次函数 的图象过原点且关于y轴对称,记函数
的图象过原点且关于y轴对称,记函数  .
.
(I)求b,c的值;
(Ⅱ)当 的单调递减区间;
的单调递减区间;
(Ⅲ)试讨论函数 y=h(x)的图象上垂直于y轴的切线的存在情况.
解:(I)∵y=ax2+(b+ )x+c-1是偶函数,
)x+c-1是偶函数,
∴b+ =0,b=-
=0,b=- ,
,
又∵图象过原点,
∴c=1,
∴b=- ,c=1,
,c=1,
(Ⅱ)当a= 时,h(x)=
时,h(x)= (
( )
)
h′(x)=
=
=
令f′(x)<0得,
函数单调递减区间是(2- ,2+
,2+ ),
),
(III)∵函数h(x)的图象上垂直于y轴的切线,
∴方程h′(x)=0存在正根,
h′(x)=
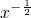 (ax2-
(ax2- x+1)+
x+1)+ (2ax-
(2ax- )=
)=
即5ax2-2x+1=0存在正根,△=4(1-5a).
①当a> 时,△<0,方程5ax2-2x+1=0无实数根,
时,△<0,方程5ax2-2x+1=0无实数根,
此时函数h(x)的图象上没有垂直于y轴的切线
②当a= 时,△=0,方程5ax2-2x+1=0根为x=1,
时,△=0,方程5ax2-2x+1=0根为x=1,
此时函数h(x)的图象上存在一条垂直于y轴的切线
③当0<a< 时,△>0,方程5ax2-2x+1=0有两个实数根x1,x2,x1+x2=
时,△>0,方程5ax2-2x+1=0有两个实数根x1,x2,x1+x2= >0,x1x2=
>0,x1x2= >0,方程5ax2-2x+1=0有两个不等的正实数根
>0,方程5ax2-2x+1=0有两个不等的正实数根
此时函数h(x)的图象上有垂直于y轴的切线
④a<0时,△>0,方程5ax2-2x+1=0有且仅有一个正实数根,此时函数h(x)的图象上存在一条垂直于y轴的切线
综上:
当a> 时,不存在垂直于y轴的切线
时,不存在垂直于y轴的切线
当a= 或a<0时,存在一条垂直于y轴的切线
或a<0时,存在一条垂直于y轴的切线
当0<a< 时,存在垂直于y轴的切线.
时,存在垂直于y轴的切线.
分析:(I)若函数的图象经过原点,则常数项为0,若函数为偶函数,则函数的图象关于y轴对称,故不难求出b,c的值.
(II)当a= 时,结合(1)的结论不难给出函数导函数的解析式,确定导函数的符号易得函数的单调区间.
时,结合(1)的结论不难给出函数导函数的解析式,确定导函数的符号易得函数的单调区间.
(III)如果函数图象上存在垂直于y轴的切线,则切点处的导数为0,结合导数即可求解.
点评:本小题主要考查二次函数的性质、函数奇偶性的应用、导数的应用等基础知识,考查待定系数法.待定系数法是求函数解析式的常用方法之一,当函数f(x)类型确定时,可用待定系数法.其解题步骤一般为:①根据函数类型设出函数的解析式(其中系数待定)②根据题意构造关于系数的方程(组)③解方程(组)确定各系数的值④将求出的系数值代入求出函数的解析式.
 )x+c-1是偶函数,
)x+c-1是偶函数,∴b+
 =0,b=-
=0,b=- ,
,又∵图象过原点,
∴c=1,
∴b=-
 ,c=1,
,c=1,(Ⅱ)当a=
 时,h(x)=
时,h(x)= (
( )
)h′(x)=

=

=

令f′(x)<0得,
函数单调递减区间是(2-
 ,2+
,2+ ),
),(III)∵函数h(x)的图象上垂直于y轴的切线,
∴方程h′(x)=0存在正根,
h′(x)=

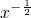 (ax2-
(ax2- x+1)+
x+1)+ (2ax-
(2ax- )=
)=
即5ax2-2x+1=0存在正根,△=4(1-5a).
①当a>
 时,△<0,方程5ax2-2x+1=0无实数根,
时,△<0,方程5ax2-2x+1=0无实数根,此时函数h(x)的图象上没有垂直于y轴的切线
②当a=
 时,△=0,方程5ax2-2x+1=0根为x=1,
时,△=0,方程5ax2-2x+1=0根为x=1,此时函数h(x)的图象上存在一条垂直于y轴的切线
③当0<a<
 时,△>0,方程5ax2-2x+1=0有两个实数根x1,x2,x1+x2=
时,△>0,方程5ax2-2x+1=0有两个实数根x1,x2,x1+x2= >0,x1x2=
>0,x1x2= >0,方程5ax2-2x+1=0有两个不等的正实数根
>0,方程5ax2-2x+1=0有两个不等的正实数根此时函数h(x)的图象上有垂直于y轴的切线
④a<0时,△>0,方程5ax2-2x+1=0有且仅有一个正实数根,此时函数h(x)的图象上存在一条垂直于y轴的切线
综上:
当a>
 时,不存在垂直于y轴的切线
时,不存在垂直于y轴的切线当a=
 或a<0时,存在一条垂直于y轴的切线
或a<0时,存在一条垂直于y轴的切线当0<a<
 时,存在垂直于y轴的切线.
时,存在垂直于y轴的切线.分析:(I)若函数的图象经过原点,则常数项为0,若函数为偶函数,则函数的图象关于y轴对称,故不难求出b,c的值.
(II)当a=
 时,结合(1)的结论不难给出函数导函数的解析式,确定导函数的符号易得函数的单调区间.
时,结合(1)的结论不难给出函数导函数的解析式,确定导函数的符号易得函数的单调区间.(III)如果函数图象上存在垂直于y轴的切线,则切点处的导数为0,结合导数即可求解.
点评:本小题主要考查二次函数的性质、函数奇偶性的应用、导数的应用等基础知识,考查待定系数法.待定系数法是求函数解析式的常用方法之一,当函数f(x)类型确定时,可用待定系数法.其解题步骤一般为:①根据函数类型设出函数的解析式(其中系数待定)②根据题意构造关于系数的方程(组)③解方程(组)确定各系数的值④将求出的系数值代入求出函数的解析式.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
 的图象过点
的图象过点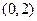 ,其导函数为
,其导函数为 ,数列
,数列
 项和为
项和为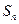 ,点
,点 在函数
在函数 .
. 的解析式;
的解析式; ,求数列
,求数列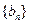 的前
的前 .
.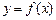 的图象过点(0,
的图象过点(0, ),且
),且 的解集为(1,3)。
的解集为(1,3)。 的解析式;
的解析式; ,
, 的最值。
的最值。 的图象过点(1,13),图像关于直线
的图象过点(1,13),图像关于直线 对称。
对称。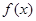 的解析式。
的解析式。 ,
, ,
, 的零点有三个,求实数
的零点有三个,求实数 的取值范围;
的取值范围; 在[
在[ ,2]上的最小值。
,2]上的最小值。 的图象过点(0,—3),且
的图象过点(0,—3),且 的解集(1,3)。
的解集(1,3)。 的解析式;
的解析式; 时,恒有
时,恒有 求实数t的取值范围。
求实数t的取值范围。