题目内容
17.已知f(x)是定义在R上且周期为6的奇函数,当x∈(0,3)时,f(x)=lg(2x2-x+m).若函数f(x)在区间[-3,3]上有且仅有5个零点(互不相同),则实数m的取值范围是$(\frac{1}{8},1]∪\{\frac{9}{8}\}$.分析 由奇函数的性质和函数的周期性,可得0、±3是函数f(x)的零点,将函数f(x)在区间[-3,3]上的零点个数为5,转化为当x∈(0,3)时,2x2-x+m>0恒成立,且2x2-x+m=1在(0,3)有一解,由此构造关于m的不等式组,解不等式组可得实数m的取值范围.
解答 解:由题意知,f(x)是定义在R上的奇函数,
所以f(0)=0,即0是函数f(x)的零点,
因为f(x)是定义在R上且以6为周期的周期函数,
所以f(-3)=f(3),且f(-3)=-f(3),则f(-3)=f(3)=0,
即±3也是函数f(x)的零点,
因为函数f(x)在区间[-3,3]上的零点个数为5,
且当x∈(0,3)时,f(x)=lg(2x2-x+m).
所以当x∈(0,3)时,2x2-x+m>0恒成立,且2x2-x+m=1在(0,3)有一解,
即$\left\{\begin{array}{l}{1-8m<0}\\{2•(\frac{1}{4})^{2}-\frac{1}{4}+m=1}\end{array}\right.$或$\left\{\begin{array}{l}{1-8m<0}\\{m≤1}\\{2•{3}^{2}-3+m-1>0}\end{array}\right.$,
解得$(\frac{1}{8},1]∪\{\frac{9}{8}\}$.
故答案为:$(\frac{1}{8},1]∪\{\frac{9}{8}\}$.
点评 本题考查奇函数的性质,函数的周期性,对数函数的性质,函数的零点的综合应用,二次函数根的分布问题,难度比较大.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
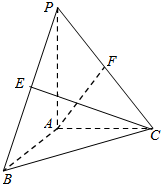 (理科做)如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠BAC=$\frac{π}{2}$,PA=AB=AC,E,F分别为棱PB,PC的中点,则异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
(理科做)如图,在三棱锥P-ABC中,已知PA⊥平面ABC,∠BAC=$\frac{π}{2}$,PA=AB=AC,E,F分别为棱PB,PC的中点,则异面直线AF与CE所成的角的余弦值为$\frac{\sqrt{3}}{6}$.